Figurat gjeometrike
Gjeometria është shkenca që studion vetitë e figurave gjeometrike.
Figurat gjeometrike janë shumë të larmishme, si për shembull: Trekëndëshi, katrori, drejtkendeshi rrethi etj.
Çdo figurë gjeometrike ne e mendojmë të përbërë prej pikash.
Pika dhe drejtëza
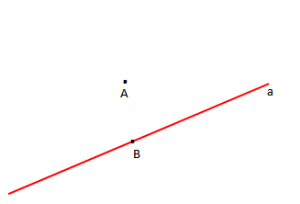
Zakonisht, drejtëzat i shënojmë me shkronja të vogla (a, b, c…), kurse pikat me shkronja të mëdha (A, B, C….).
Pika B shtrihet në drejtëzën a; themi ndryshe: “drejtëza a kalon nëpër pikën B” dhe e shënojmë .
Pika A nuk shtrihet në drejtëzën a; themi ndryshe: “drejtëza a nuk kalon nëpër pikën A” dhe shënojmë
/h2>
Segmenti

Pikat A, B, C shtihen në pikën a.
Pjesa e drejtëzës nga pika A deri në pikën C quhet segmenti AC dhe shënohet [AC] ose [CA].
Ka vend vetia themelore: “Nga tri pika të një drejtëze, njëra dhe vetëm njëra ndodhet ndërmjet dy të tjerave”.
Gjysmëdrejtëza, Gjysmëplani, Këndi
- Gjysmëdrejtëza
Gjysmëdrejtëz quhet pjesa e drejtëzës e përbërë nga një pikë ë dhënë e saj dhe gjithë pikat e drejtëzës, që ndodhen nga e njëjta anë e kësaj pike. Pika e dhënë quhet origjinë e gjysmëdrejtëzës.
Dy gjysmëdrejtëza të ndryshme të të njëjtës drejtëz, që kanë të njëjtën origjinë quhen gjysmëdrejtëza plotësuese.
Shohim figurat:
![]()
![]()

- Gjysmëplani
Drejtëza e ndan planin në dy gjysmëplane, në mënyrë që:
- Çdo pikë jashtë drejtëzës i takon njërit gjysmëplan.
- Nëse skajet e një segmenti ndodhen në njërin gjysmëplan, atëherë segmenti nuk e prêt drejtëzën.
- Nëse skajet e një segmenti ndodhen në gjysmëfinale të ndryshëm, atëherë segmenti e prêt drejtëzën.
- Këndi
Përkufizim: “Kënd quhet figura gjeometrike e përbërë nga dy gjysmëdrejtëza, që kanë të njëjtën origjinë“.
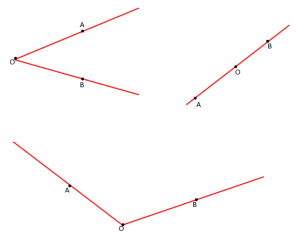
- Nëse brinjët e këndit janë gjysmëdrejtëza plotësuese, këndi quhet i shtrirë.
- Nëse këndi nuk është i shtrirë, njëra nga pjesët quhet e brendshme, kurse tjetra pjesë e jashtme e këndit.
Kongruenca e segmenteve dhe këndeve
- Kongruenca e figurave gjeometrike
Përkufizim: “Në gjeometri, figurat që kanë të njëjtën formë dhe të njëjtat përmasa quhen kongruente”.
- Kongruenca e segmenteve
Ka vend kjo veti themelore: “Në gjysmëdrejtëzën e çfarëdoshme me origjinë O gjendet një dhe vetëm një pikë M, e tillë që segmenti [OM] të jetë kongruent me një segment të dhënë”.
- Kongruenca e këndeve
Për kongruencën e këndeve, ka vend vetia themelore: “Në njërin nga gjysmëplanet e përcaktuar nga drejtëza e çfarëdoshme (OA), gjendet vetëm një rreze (OB), e tillë që këndi të jetë kongruent me një kënd të dhënë”.
Përkufizim: “Gjysmëdrejtëza që del nga kulmi i këndit dhe e ndan atë në dy kënde kongruentë, quhet përgjysmore e këndit”.