
Teorema e Langranzhit
Teorema e Langranzhit thotë: Nëse funksioni f është i derivueshëm në intervalin I dhe ,
janë dy pika çfarëdo të kërij intervali, atëherë ekziston të paktën një pikë c, ndërmjet pikave
,
e tillë që:
.
Ndryshe e shkruajmë:
.
Shembull 1
Për funksionin , të gjendet pika që vërteton teoremën e langranzhit në segmentin
.
Zgjidhje
Gjejmë në fillim dhe
:
Gjejmë :
Zbatojmë teoremën e langranzhit për të gjetur pikën c:
Do të kemi:
Studimi i monotonisë së funksionit
Teorema 1: Nëse funksioni ka derivat pozitiv në çdo pikë të intervalit I, atëherë ky funksion është rritës në intervalin I.
Teorema 2: Nëse funksioni f ka derivat negativ në çdo pikë të intervalit I, atëherë ky funksion është zbritës në intervalin I.
Shembull 2
Studioni monotonin e funksionit
Zgjidhje
Gjejmë në fillim derivation e funksionit y:
Gjejmë rrënjën e derivatit duke e barazuar atë me zero:
.
Studiojmë shenjën e derivatit:
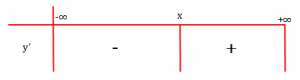
Pra, siç shihet, për intervalin funksioni është zbritës, ndërsa për intervalin
funksioni është rritës.
Teorema Ferma
Metodë
Për të studiuar monotoninë e një funksioni numerik f:
- Gjendet bashkësia e percaktimit E.
- Gjendet bashkësia
ku funksioni është i derivueshëm.
- Njehsohet
dhe studiohet shenja e tij në bashkësinë
.
- Duke parë intervalet e
ku
ruan shenjë, nxirren përfundimet për intervalet e monotonisë së funksionit f.
Teorema Ferma: Nëse funksioni f, i derivueshëm në intervalin I, ka ekstremum në pikën , atëherë
.
Shembull 3
Të gjendet bashkësia e përcaktimit dhe të studiohet monotonia e funksionit .
Zgjidhje
Gjejmë bashkësinë e përcaktimit E:
Pra, .
Për të gjetur monotonin e funksionit, gjejmë në fillim derivatin e tij:
Gjejmë bashkësinë ku funksioni është i derivueshëm:
.
Pra, .
Barazojmë me zero derivatin që gjetëm:
Shohim që ky derivat nuk bëhet kurrë zero, por ka pikë këputje në pikën x=2.
Studiojmë shënjën, e cila varet vetëm nga emëruesi:
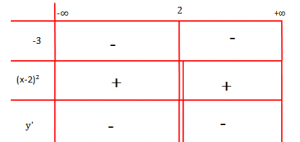
Emëruesi është gjithmonë pozitiv sepse është fuqi e një numri çift, ndërsa derivati y’ është negativ sepse emëruesi është numër negativ.

