Sisteme ekuacionesh me dy te panjohura | Matematika 10

Sisteme ekuacionesh te fuqise se pare me dy te panjohura

Sistemi me lart quhet sistem ekuacionesh të fuqisë së parë me dy të panjohura.

Përkufizim 1: “Zgjidhje të sistemit quhen të gjitha çiftet (x, y), që po të zëvëndësohen tek sistemi, ekuacionet kthehen në barazime numerike të vërteta”.

Përkufizim 2: “Të zgjidhësh një sistem do të thotë të gjesh të gjitha zgjidhjet e sistemit”.

Ekzistojnë tri mënyra për të zgjidhur sistemet e ekuacioneve të fuqisë së parë me dy ndryshore:

1. Menyra e zëvëndësimit.
2. Metoda e eleminimit të njërës prej prej të panjohurave (menyra e mbledhjes).
3. Mënyra grafike.

Shembull 1

Të zgjidhet me metodën e eleminimit të një prej të panjohurave sistemi

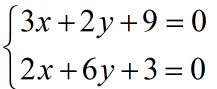
Zgjidhje

Për të eleminuar të panjohuren y shumëzojmë ekuacionin e parë me -3.

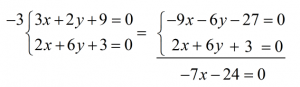
Pra, kemi ekuacionin $\displaystyle -7x-24=0$

$\displaystyle 7x+24=0$

$\displaystyle x=\frac{24}{7}$

Tani zëvëndësojmë x-in tek ekuacioni dhe gjejmë y-in:

$\displaystyle 3\cdot \frac{24}{7}+2y+9=0$

Shumëzojmë të dy anët me 7 dhe do të kemi:

$\displaystyle 72+14y+63=0$

$\displaystyle 14y=-135$

$\displaystyle y=-\frac{135}{14}$ .

Përfundim: Zgjidhje e sistemit është çifti $\displaystyle \left( \frac{24}{7},-\frac{135}{14} \right)$ .

Per me shume shembuj te zgjidhur me ekuacionet e fuqise se pare me nje ndryshore shikoni Ushtrime te zgjidhura – Ekuacione

Sisteme ekuacionesh të fuqisë së dytë me dy të panjohura

Pwrkufizim: “Nëse një nga ekuacionet e sistemit është i fuqisë së dytë sistemi quhet i fuqisë së dytë“.

Shembull 1

Të zgjidhet sistemi

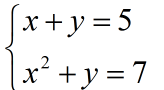
Zgjidhje

Përdorim metodën e zëvëndësimit.

Tek ekuacioni i parë zëvëndësojmë x-in:

$\displaystyle x+y=5$

$\displaystyle x=5-y$

Duke zëvëndësuar x-in tek ekuacioni i dytë do të kemi:

$\displaystyle {{\left( 5-y \right)}^{2}}+y=7$

$\displaystyle 25-10y+{{y}^{2}}+y=7$

$\displaystyle {{y}^{2}}-9y+18=0$

Duke zgjidhur ekuacionin e dytë, gjejmë rrënjët e tij $\displaystyle {{y}_{1}}=6$ dhe $\displaystyle {{y}_{2}}=3$ .

Për të gjetur vlerat e x-it, zëvëndësojmë y-in tek ekuacioni i parë dhe gjejmë vlerat:

$\displaystyle {{x}_{1}}=5-6=-1$

$\displaystyle {{x}_{2}}=5-3=2$

Përfundim: Zgjidhje e sistemit është bashkësia $\displaystyle A=\left\{ \left( -1,6 \right),\left( 2,3 \right) \right\}$