Perkulshmeria e funksionit. Pikat e infleksionit

Perkulshmeria e funksionit

Përkufizim 1: Nëse tangjentja në çdo pikë të vijës $\displaystyle l$ ndodhet nën vijë, atëherë vija $\displaystyle l$ quhet e lugët në I.

Përkufizim 2: Nëse tangjentja në çdo pikë të vijës $\displaystyle l$ ndodhet mbi vijë, atëherë vija $\displaystyle l$ quhet e mysët në I.

Përkufizim 3: Pika e vijës $\displaystyle l$ që lidh një pjesë të lugët me një pjesë të mysët të saj quhet pikë infleksioni e vijës.

Teorema 1:

a) Në qoftë se funksioni f ka derivat të dytë $\displaystyle f''\left( x \right)$ që është pozitiv për çdo vlerë të x-it nga intervali I, atëherë grafiku i këtij funksioni është i lugët në I.

b) Në qoftë se funksioni f ka derivat të dytë $\displaystyle f''\left( x \right)$ që është negativ për çdo vlerë të x-it nga intervali I, atëherë grafiku i këtij funksioni është i mysët në I.

Teorema 2: Në qoftë se funksioni f ka derivat të dytë në çdo pikë të intervalit $\displaystyle \left] a,b \right[$ dhe derivati i dytë ndërron shenjë, duke kaluar nga intervali $\displaystyle \left] a,c \right[$ në intervalin $\displaystyle \left] b,c \right[$ , atëherë pika C me abshisë c është pikë infleksioni për grafikun e këtij funksioni.

Ushtrime te zgjidhura

Ushtrimi 1

Të shqyrtohet perkulshmeria dhe të gjenden pikat e infleksionit ër grafikun e funksionit

a) $\displaystyle y=25-{{x}^{2}}$

b) $\displaystyle y=-2{{x}^{2}}-7x+2$

Zgjidhje

a) $\displaystyle y=25-{{x}^{2}}$

Gjejmë derivatin e parë pastaj derivatin e dytë për funksionin tonë:

$\displaystyle y'=-2x$

$\displaystyle y''=-2$ .

Për çdo vlerë të x ky funksion është konstant -2, pra është i mysët.

b) $\displaystyle y=-2{{x}^{2}}-7x+2$

$\displaystyle y'=-4x-7$

$\displaystyle y''=-4$ .

Për çdo vlerë të x ky funksion është konstant -4, pra është i mysët.

Ushtrimi 2

Të shqyrtohet perkulshmeria dhe të gjenden pikat e infleksionit për grafikun e funksionit

a) $\displaystyle y=-4{{x}^{4}}+2{{x}^{2}}-3$

b) $\displaystyle y=\frac{5}{x-3}$

Zgjidhje

a) $\displaystyle y=-4{{x}^{4}}+2{{x}^{2}}-3$

$\displaystyle y'=-16{{x}^{3}}+4x$

$\displaystyle y'=-48{{x}^{2}}+4$

Barazojmë me zero derivatin e dytë dhe studiojmë shenjën:

$\displaystyle -48{{x}^{2}}+4=0$

$\displaystyle -12{{x}^{2}}+1=0$

$\displaystyle {{x}^{2}}=\frac{1}{12}$

$\displaystyle x=\pm \sqrt{\frac{1}{12}}$

Pra, kemi :

$\displaystyle {{x}_{1}}=-\frac{1}{2\sqrt{3}}$

$\displaystyle {{x}_{2}}=\frac{1}{2\sqrt{3}}$

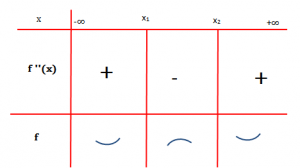
Pra, nga grafiku shikojmë që funksioni është i lugët në $\displaystyle \left] -\infty ,-\frac{1}{2\sqrt{3}} \right[\cup \left] \frac{1}{2\sqrt{3}},+\infty \right[$ dhe i mysët në $\displaystyle \left] -\frac{1}{2\sqrt{3}},\frac{1}{2\sqrt{3}} \right[$ .

b) $\displaystyle y=\frac{5}{x-3}$

$\displaystyle y'=\frac{0-5}{{{\left( x-3 \right)}^{2}}}=-\frac{5}{{{\left( x-3 \right)}^{2}}}$

$\displaystyle y''=\frac{10x}{{{\left( x-3 \right)}^{4}}}$

Barazojmë me zero derivatin e dytë dhe studiojmë shenjën:

$\displaystyle \frac{10x}{{{\left( x-3 \right)}^{4}}}=0$ për çdo $\displaystyle x\ne 3$ .

$\displaystyle x=0$ .

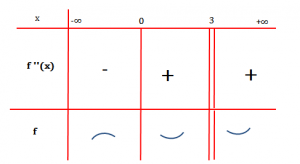
Siç duket nga figura, funksioni është i lugët për $\displaystyle x\in \left] -\infty ,3 \right[$ dhe i mysët për $\displaystyle x\in \left] 3,+\infty \right[$ .