Rombi

vetite e rombit

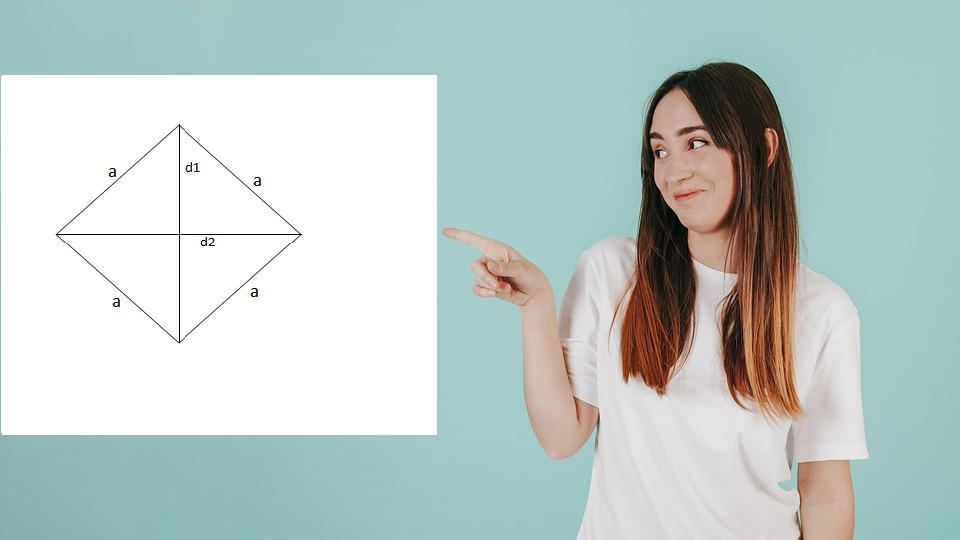
Përkufizim: “Romb quhet paralelogrami që i ka të katër brinjët kongruente”.

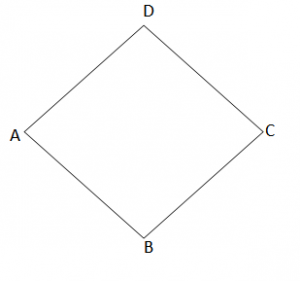
rombi

Rombi

AB = BC = CD = DA

Rombi është paralelogram dhe zotëron gjithe vetitë e tij që përmendëm më lart dhe ka këto veti të tjera:

Vetia 1: “Rombi i ka diagonalet pingule ndërmjet tyre”.

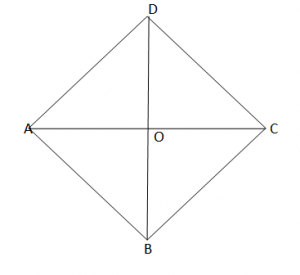
ROMBI-DIAGONALET

$\displaystyle AC\bot BD$

Vetia 2: “Rombi i ka diagonalet përgjysmore të këndeve të tij”.

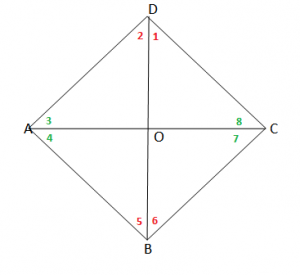
ROMBI-DIAGONALET-pergjysmojne

$\displaystyle \angle 1=\angle 2=\angle 5=\angle 6$

$\displaystyle \angle 3=\angle 4=\angle 7=\angle 8$

Vetia 3: “Diagonalet e rombit, e ndajnë rombin në katër trekëndësha kongruentë”.

ROMBI-DIAGONALET

$\displaystyle \vartriangle AOB=\vartriangle BOC=\vartriangle COD=\vartriangle DOA$

Kushtet që një paralelogram të jetë romb:

Kur diagonalet e tij janë pingule.
Kur njëra nga diagonalet e tij të përgjysmoj njërin kënd.

Perimetri i rombit

Perimetri i rombit gjendet duke mbledhur gjitha brinjët e tij.

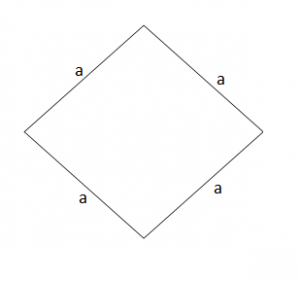
Pra do të kemi:

P = a + a + a + a

P = 4 ∙ a

Shembull 1

Gjeni perimetrin e rombit me brinje 20 cm.

Zgjidhje

Nga formula e perimetrit, dimë që:

P = 4 ∙ a

Pra, do të kemi:

P = 4 ∙ a

P = 4 ∙ 20

P = 20 cm.

Shembull 2

Gjeni brinjën e rombit me perimetër 36 cm

Zgjidhje

Nga formula e perimetrit, dimë që:

P = 4 ∙ a

Bëjmë zëvëndësimet:

36 = 4 ∙ a

$\displaystyle a=\frac{36}{4}$

a = 9 cm.

Siperfaqja e rombit

Sipërfaqja e rombit gjendet duke shumëzuar dy diagonalet me njëra-tjetrën dhe duke i pjestuar me 2.

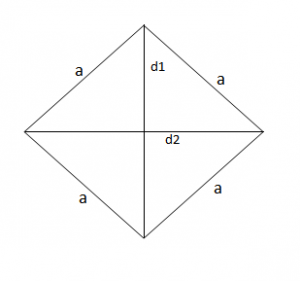
Pra, do të kemi:

$\displaystyle S=\frac{{{d}_{1}}\cdot {{d}_{2}}}{2}$

Shembull 1

Gjeni sipërfaqen e rombit me diagonal 5 cm dhe 8 cm

Zgjidhje

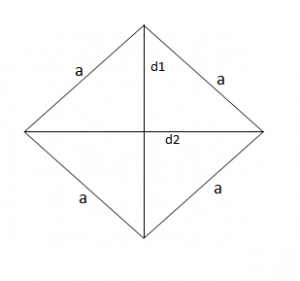
Nga formula e siperfaqes, dimë që:

$\displaystyle S=\frac{{{d}_{1}}\cdot {{d}_{2}}}{2}$

Atëherë, do të kemi:

$\displaystyle S=\frac{5\cdot 8}{2}$

$\displaystyle S=\frac{40}{2}$

$\displaystyle S=20c{{m}^{2}}$

Shembull 2

Gjeni brinjët e rombit, duke ditur që siperfaqja e tij është 100 $\displaystyle c{{m}^{2}}$ dhe njëra diagonale është sa gjysma e diagonals tjetër.

Zgjidhje

Kemi të dhënë:

S = 100 $\displaystyle c{{m}^{2}}$

$\displaystyle {{d}_{2}}=\frac{1}{2}{{d}_{1}}$

Nga formula e siperfaqes, dimë që:

$\displaystyle S=\frac{{{d}_{1}}\cdot {{d}_{2}}}{2}$

Bëjmë zëvëndësimet:

$\displaystyle 100=\frac{{{d}_{1}}\cdot \frac{1}{2}{{d}_{1}}}{2}$

$\displaystyle 100=\frac{\frac{{{d}_{1}}^{2}}{2}}{2}$

$\displaystyle 100=\frac{{{d}_{1}}^{2}}{4}$

$\displaystyle {{d}_{1}}^{2}=400$

$\displaystyle {{d}_{1}}=20$

Gjetëm $\displaystyle {{d}_{1}}$ , tani gjejmë dhe $\displaystyle {{d}_{2}}$ :

$\displaystyle {{d}_{2}}=\frac{1}{2}{{d}_{1}}$

$\displaystyle {{d}_{2}}=\frac{1}{2}20$

$\displaystyle {{d}_{2}}=10$ cm.