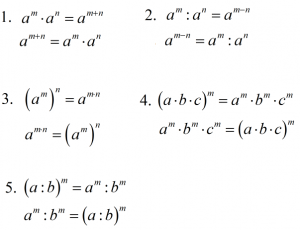
Keto ushtrime bazohen tek vetite e fuqive (kliko linkun per te lexuar).
Më poshtë keni 5 vetite e fuqive dhe barazimet e anasjellta të tyre:

vetite e fuqive
Ushtrimi 1 (pika a dhe b e zgjidhur)
Duke njohur vetite e fuqive, gjeni me dy mënyra vlerën e shprehjeve më poshtë:
a) Mënyra 1
Mënyra 2
b) Mënyra 1
Mënyra 2
c)
d)
e)
f)
g)
Ushtrimi 2 (pika a e zgjidhur)
Paraqit shprehjet e mëposhtme si prodhim faktorësh me një eksponent:
a)
b)
c)
d)
Ushtrimi 3
Ktheni në fuqi me bazë 4:
Ushtrimi 4
Ktheni në fuqi me bazë 3:
Shndërrojmë bazat 27 dhe 9 në fuqi me bazë 3:
dhe
Atëherë shkruajmë:
Ushtrimi 5
Transformoni në fuqi me bazat e tyre:
a)
b)
c)
shndërrojmë 25 si fuqi me bazë 5:
Pra, do të kemi:
Ushtrimi 6
Gjeni vlerën e shprehjeve:
Në fillim vëmë re se shprehja në kllapat gjarpërueshe është e gjitha në fuqi 0, që do të thotë se vlera e saj është 1.
Tani sh ndërrojmë gjithë shprehjen e mbetur si fuqi me bazë 2.
Do të kemi:
Ushtrimi 7
Gjeni vlerën e shprehjeve:

