Ushtrime te zgjidhura – Kongruenca e trekendeshave

Duke u bazuar tek kongruenca e trekëndëshave, zgjidhim ushtrimet më poshtë.

Ushtrimi 1

Segmentet [AC] dhe [BD] priten në mesin e tyre. Vërtetoni që $\displaystyle \vartriangle ABC=\vartriangle CDA$

Zgjidhje

Ndërtojmë figurën:

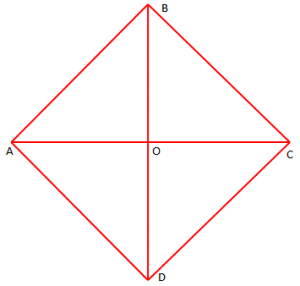
Kemi të dhënë:

AO = OC
BO = OD
[BD] permesore e [AC]
[AC] permesore e [BD]

Meqë pikat B dhe D janë të baraslarguara nga [AC], atëherë mund të themi që AB = BC = VD = DA

Pra, kemi:

AB = AD nga vetia e permesores
BC = CD nga vetia e permesores
$\displaystyle \angle ABC=\angle CDA$ nga vetia e permesores

Nga rasti I i kongruencës së trekëndëshave (BKB), kemi $\displaystyle \vartriangle ABC=\vartriangle CDA$ .

Ushtrimi 2

Jepet trekëndëshi ABC. Në bazën BC të tij janë marrë pikat M, N të tilla që BM = CN.

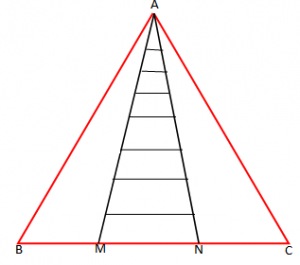
Vërtetoni që:

a) $\displaystyle \vartriangle BAM=\vartriangle CAN$ .

b) Trekëndëshi AMN është dybrinjëshëm.

Zgjidhje

a) Marrim në shqyrtim trekëndëshat BAM dhe CAN.

Kemi:

AB = AC si brinjë anësore të trekëndëshit dybrinjëshëm
BM = NC të dhënë nga ushtrimi.
$\displaystyle \hat{B}=\hat{C}$ nga teorema e trekëndëshit dybrinjëshëm, ku këndet pranë bazës janë kongruente.

Në bazë të rastit të parë të kongruencës së trekëndëshave, kemi: $\displaystyle \vartriangle BAM\equiv \vartriangle CAN$

b) Nga kongruenca e trekëndëshave, dimë që: “Në trekëndëshat kongruentë, përballë brinjëve kongruente ndodhen këndet kongruente dhe përballë këndeve kongruente ndodhen brinjët kongruente”.
Përballë këndëve B dhe C ndodhen brinjët AM dhe AN, ndaj kemi AM = AN.

Pra, vërtetuam që trekëndëshi AMN është dybrinjëshëm.

Ushtrimi 3

Në përgjysmoren e këndit A është marrë pika M, kurse në brinjët e tij pikat B, C, të tilla që $\displaystyle \angle AMB=\angle AMC$ .

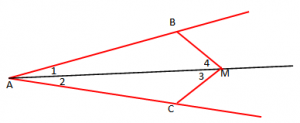
Vërtetoni që AC = AB.

Zgjidhje

Marrim në shqyrtim trekëndëshat AMB dhe AMC.

Kemi:

$\displaystyle \hat{1}=\hat{2}$ nga vetia e përgjysmores.
AM brinjë e përbashkët.
$\displaystyle \hat{3}=\hat{4}$ të dhënë nga ushtrimi.

Nga rasti i dytë i kongruencës së trekëndëshave, kemi: $\displaystyle \vartriangle AMB=\vartriangle AMC$

Nga kongruenca e trekëndëshave, dimë që: “Në trekëndëshat kongruentë, përballë brinjëve kongruente ndodhen këndet kongruente dhe përballë këndeve kongruente ndodhen brinjët kongruente”.

Përballë këndeve 3 dhe 4 ndodhen përkatësisht brinjët AC dhe AB, ndaj kemi AC = AB.

Ushtrimi 4

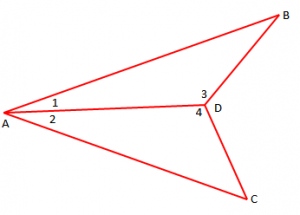
Në figurën më poshtë kemi $\displaystyle \hat{1}=\hat{2}$ dhe $\displaystyle \hat{3}=\hat{4}$ dhe BD = 10 cm.

Gjeni CD.

Zgjidhje

Marrim në shqyrtim trekëndëshat ABD dhe ACD.

Kemi:

$\displaystyle \hat{1}=\hat{2}$ të dhënë nga ushtrimi
AD brinjë e përbashkët e trekëndëshave.
$\displaystyle \hat{3}=\hat{4}$ të dhënë nga ushtrimi.

Nga rasti i dytë i kongruencës së trekëndëshave (KBK) kemi: $\displaystyle \vartriangle ADB=\vartriangle ACD$

Përballë këndeve 1 dhe 2 kemi përkatësisht brinjët BD dhe CD, ndaj kemi BD = CD = 10 cm.

Ushtrimi 5

Kemi të dhënë trekëndëshin ABC. Në segmentin [AB] është hequr permesoreja K.

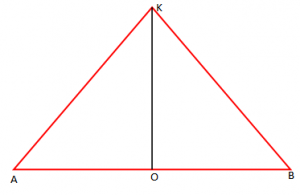
Vërtetoni që trekëndëshat AOK dhe BOK janë kongruentë.

Zgjidhje

Marrim në shqyrtim trekëndëshat AOK dhe BOK.

Kemi:

KO brinjë e përbashkët
AO = BO nga vetia e permesores
AK = BK nga vetia e permesores

Nga rasti III i kongruencaës së trekëndëshave, kemi: $\displaystyle \vartriangle AOK\equiv \vartriangle BOK$

Ushtrimi 6

Trekëndëshat dybrinjëshëm ADC dhe CBD kanë bazë të përbashkët [DC]. Drejtëza (AB) e pret segmentin [CD] në pikën M.

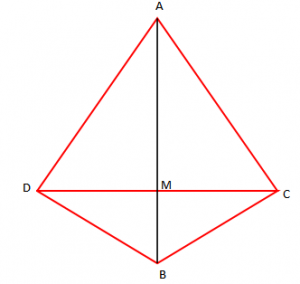
Vërtetoni që:

a) $\displaystyle \vartriangle ADB\equiv \vartriangle ACB$

b) $\displaystyle MD=MC$

Zgjidhje

a) Marrim nq shqyrtim trekëndëshat ADB dhe ACB.

Kemi:

AB brinjë e përbashkët.
AD = AC si brinjë anësore të trekëndëshit ADC
DB = CB si brinjë anësore të trekëndëshit BCD

Nga rasti III i kongruencës së trekëndëshave (BBB), kemi: $\displaystyle \vartriangle ADB\equiv \vartriangle ACB$ .

Nga kongruenca e trekendëshave dimë që: “Në trekëndëshat kongruentë, përballë brinjëve kongruente ndodhen këndet kongruente dhe përballë këndeve kongruente ndodhen brinjët kongruente”.

Përballë brinjëve BD dhe BC ndodhen përkatësisht këndet BAD dhe BAC, ndaj $\displaystyle \angle BAD=\angle BAC$ .

Marrim në shqyrtim trekëndëshat AMD dhe AMC.

Kemi:

AD = AC si brinjë anësore të trekëndëshit dybrinjëshëm ADC.
$\displaystyle \angle BAD=\angle BAC$
AM brinjë e përbashkët e trekëndëshave.

Nga rasti i parë i kongruencës së trekëndëshave, kemi: $\displaystyle \vartriangle AMD=\vartriangle AMC$ .

Nga kongruenca e trekendëshave dimë që: “Në trekëndëshat kongruentë, përballë brinjëve kongruente ndodhen këndet kongruente dhe përballë këndeve kongruente ndodhen brinjët kongruente”.

Përballë këndeve DAM dhe CAM ndodhen përkatësisht brinjët MD dhe CM, ndaj MD = CM.