Shumekendeshat, Figurat Gjeometrike , matematika 6

Shumekendeshat

Shumekendeshat janë pjesa e planit e kufizuar nga një vijë e thyer e mbyllur së bashku me vijën.

Shumekendeshat emërtohen në varësi të numrit të brinjëve që ata kanë.

Kujtojmë:

Shumëkëndëshi qe i ka brinjët të barabarta dhe këndet e barabarta, quhet shumëkëndësh i rregullt.

Trekëndëshi barabrinjës dhe katrori janë shumëkëndësha të rregullt.

Trekëndëshat dhe vetitë e tyre

Shumekendeshat që kanë tre brinjë quhen trekëndësha.

Trekëndëshat i klasifikojmë sipas gjatësisë së brinjëve dhe sipas masës së këndeve.

Shumekendeshat - trekendeshi barabrinjes

Barabrinjës – të tria brinjët i ka të barabarta

shumekendeshat - trekendeshi dybrinjeshem

Dybrinjëshëm – ka dy brinjë të barabarta

Brinjëndyshëm – të tria brinjët i ka të ndryshme

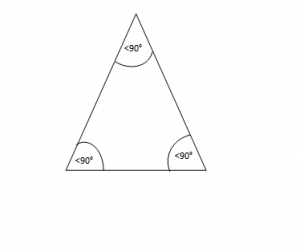
Këndngusht – të tria këndet i ka të ngushta

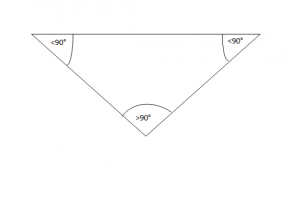
Këndgjerë – ka një kënd të gjerë.

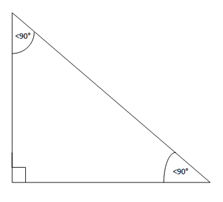
Kenddrejt – Ka një kend të drejt

Për me shumë mbi trekëndëshat, klikoni KETU

Katerkendeshat

Shumekendeshi me katër brinjë quhen katërkëndësh.

Disa katërkëndësha kanë disa veti të veçanta. Ne përdorim vetit e brinjëve dhe këndeve për të emërtuar katërkëndësha të ndryshëm.

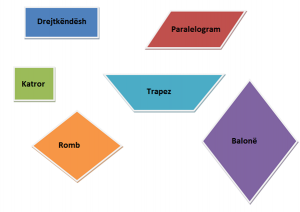
Katrorët, drejtkëndëshat, paralelogramët, rombet, trapezët dhe balonat janë katërkëndësha me veti speciale.

figurat gjeometrike

Paralelogrami:

Përkufizim: Paralelogrami është një katërkëndësh qe që i ka brinjët dy e nga dy të barabarta dhe paralele.

paralelogrami

Vetitë:

Brinjët përballë janë paralele (nga përkufizimi)
Brinjët përballë janë kongruente (nga përkufizimi)
Diagonalja e paralelogramit e ndanë atë në dy trekëndësha kongruent.
Diagonalet e paralelogramit përgjysmojnë njëra – tjetrën.
Pika e prerjes së diagonaleve ështëqendër simetrie për secilen diagonal.
Këndet e kundërt janë kongruent.
Këndet e njëpasnjëshme janë kënde shtues (shuma e tyre është 180 gradë).
Pingulja e hequr mbi njëren brinjë quhet lartësi (h).
Perimetri i paralelogramit është: P = P = 2 ∙ a + 2 ∙ b = 2 ∙ (a+b).
Sipërfaqja e paralelogramit është: $S=\frac{a\cdot h}{2}$

Drejtkendeshi

Përkufizim: Drejtkendësh quhet ai paralelogram që ka njërin kënd të drejt.

Vetitë:

Diagonalet e drejtkëndëshit janë kongruente.
Sipërfaqja e drejtkëndëshit është: S = a ∙ b
Perimetri i drejkëndëshit është: P = 2 ∙ a + 2 ∙ b = 2 ∙ (a+b).

Rombi

Përkufizim: Romb quhet paralelogrami që i ka të katër brinjët të barabarta.

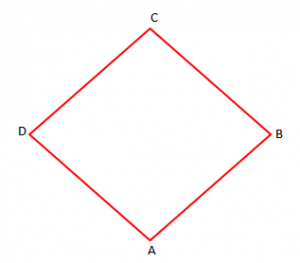
Vetitë:

Diagonalet e rombit janë përgjysmore të këndeve të tij.
Diagonalet e rombit janë pingule me njera – tjetrën.
Diagonalet e ndajnë rombin në 4 trekëndësha kongruent.
Perimetri i rombit është: P = 4 ∙ a
Sipërfaqja e rombit është: $S=\frac{d1\cdot d2}{2}$

Katrori

Përkufizim: Katror quhet rombi që ka një kënd të drejt.

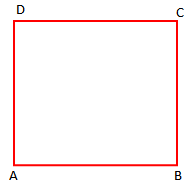
Vetitë:

Këndet janë të gjithë të drejt (nga përkufizimi).
Brinjët janë të barabarta (nga përkufizimi)
Diagonalet janë të barabarta dhe pingule me njëra-tjetrën.
Diagonalet përgjysmojnë njëra-tjetrën.
Perimetri i katrorit është: P = 4 ∙ a
Sipërfaqja e katrorit është:
Kur kemi të dhënë brinjën: S = a ∙ a ose $S={{a}^{2}}$
Kur kemi të dhënë diagonalen: $S=\frac{d\cdot d}{2}$

Trapezi

Përkufizim:Trapez quhet paralelogrami që ka një çift brinjësh paralele.

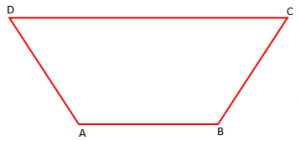
Vetitë:

Brinjët paralele quhen baza (baza e madhe dhe baza e vogël (B, b))
2 brinjët e tjera quhen brinjë anësore.
Drejtësat pingule mbi bazat quhet lartesi (h)
Perimetri I trapezit është: P = a+b+c+d
Sipërfaqja e trapezit është: $S=\frac{(B+b)\cdot h}{2}$

Për më shumë mbi katërkëndëshat, shikoni Paralelogrami, drejtkendeshi, rombi, katrori

Ushtrimi 1

Gjeni perimetrin dhe sipërfaqen e figurave të mëposhtme:

a) Katrori me brinjë 5 cm

b)Rombi me brinjë 5 cm, diagonalet respektivisht 3 cm dhe 4 cm.

c) Drejtkëndëshi me gjatësi 5 cm dhe gjerësi 3 cm

d) Paralelogrami me gjatësi 7 cm, gjerësi 4 cm dhe lartësi 3 cm.

e) Trapezi me bazën e madhe 8 cm, bazën e vogël 4 cm, brinjët anësore 3 cm dhe 5 cm si dhe lartësi 3 cm.

Zgjidhje:

P = 4 ∙ a

P = 4 ∙ 5 = 20 cm

S = a ∙ a = 5 ∙ 5 = $25c{{m}^{2}}$

Përgjigje: Perimetri i këtij katrori është 20 cm, ndërsa sipërfaqja është $25c{{m}^{2}}$

P = 4 ∙ a

P = 4 ∙ 6 = 20 cm

$S=\frac{d1\cdot d2}{2}$

$S=\frac{3\cdot 4}{2}=\frac{12}{2}=6c{{m}^{2}}$

Përgjigje: Perimetri i këtij është 20 cm, kurse sipërfaqja është $6c{{m}^{2}}$ .

P = 2 ∙ (a+b).

P = 2 ∙ (5+3)=2 ∙ 8 = 16 cm

S = a ∙ b

S = 5 ∙ 3 = 15 $c{{m}^{2}}$

Përgjigje: Perimetri i këtij drejtkëndëshi është 16 cm, ndërsa sipërfaqja është 15 $c{{m}^{2}}$ .

P = 2 ∙ (a+b).

P = 2 ∙ (7+4)=2 ∙ 11 = 22 cm.

$S=\frac{a\cdot h}{2}$

$S=\frac{7\cdot 3}{2}=\frac{21}{2}=11.5c{{m}^{2}}$

Përgjigje:Perimetri i këtij paralelogrami është 22 cm, ndërsa sipërfaqja është $11.5c{{m}^{2}}$

P = a+b+c+d

P = 8+3+4+5=11+9=20 cm.

$S=\frac{(B+b)\cdot h}{2}$

$S=\frac{(8+4)\cdot 3}{2}=\frac{12\cdot 3}{2}=\frac{36}{2}=18c{{m}^{2}}$

Përgjigje:Perimetri i këtij trapezi është 20 cm, ndërsa sipërfaqja është $18c{{m}^{2}}$