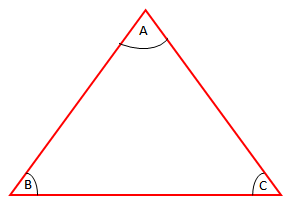
Shuma e masave te kendeve te trekendeshit

shuma e kendeve te trekendeshit - feature

Teoremë: “Shuma e masave të kendeve te trekendeshit është 180º”.

Pra, do të kemi: $\displaystyle \angle A+\angle B+\angle C$ .

Shembull 1

Në trekëndëshin dybrinjëshëm këndi në kulm është 80º. Sa është këndi në bazë në këtë trekëndësh?

Zgjidhje

Kemi:

$\displaystyle \angle A=80{}^\text{o}$

Nga trekëndëshi dybrinjëshëm dimë që këndet e bazës janë të barabarta dhe nga teorema dimë që shuma e kendeve te trekendeshit është 180º.
Shënojmë me x këndet e bazës dhe e shndërrojmë në ekuacion. Do të kemi:
$\displaystyle x+x+80=180$
$\displaystyle 2x=100$
$\displaystyle x=50{}^\text{o}$

Pra, këndet e bazës janë 50º.

Përkufizim: “Kënd i jashtëm i trekëndëshit, quhet këndi që është shtues me ndonjë kënd të trekëndëshit”.

Për shembull, kemi figurën më poshtë:

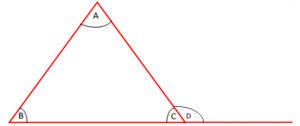
Në trekëndëshin ABC, këndi D quhet kënd i jashtëm sepse $\displaystyle \hat{C}+\hat{D}=180{}^\text{o}$ .

Teoremë: “Këndi i jashtëm i trekëndëshit është i barabartë me shumën e dy kendeve të brendshëm jo afërndenjës me të”.

Si rrjedhim, këndi i jashtëm është më i madh se çdo kënd i brendshëm jo afërndenjës me të.

Krahasimi i brinjëve dhe kendeve te trekendeshit

Teoremë 1: “Në trekëndësh, përballë brinjës më të madhe ndodhet këndi më i madh”.

Tek trekëndëshi ABC, nëse brinja BC është me e madhe se AB dhe AC, atëherë këndi A është këndi më i madh i tij.

Teoremë 2: “Në trekëndësh, përballë këndit më të madh ndodhet brinja më e madhe”.

Tek trekëndëshi ABC, nëse këndi A është këndi më i madh i trekëndëshit, atëherë brinja BC është brinja më e madhe e tij.

Mosbarazimi i trekëndëshit

Teoremë: “ Çdo brinjë e një trekëndëshi është me e vogël se shuma e dy të tjerave ”.

Rrjedhim: Për çdo tri pika A, B, C, që nuk shtrihen në një drejtëz, janë të vërteta mosbarazimet:

$\displaystyle AB<AC+CB$
$\displaystyle AC<AB+CB$
$\displaystyle BC<AB+AC$

Postime te ngjashme: