Perkufizimi, Aksioma, Teorema. Kendet e kundert ne kulm

perkufizimi - feature

Perkufizimi. Aksioma. Teorema

Perkufizimi

Ne kemi treguar saktë kuptimin e ri “kende shtues”, nëpërmjet kuptimeve të njohura që më parë: Kend, brinjë, gjysmedrejtez, gjysmëdrejtëza plotësuese. Në këtë mënyrë themi që është dhënë përkufizimi i “kende shtues”.

Aksiomat

Më herët, ju jeni njohur me teoremat, që janë fjali matematika të vërteta.

Përkufizim: “Aksiomë quhet fjalia matematike, vërtetësia e të cilës pranohet pa vërtetim”.

Teoremat

Përkufizim: “Fjalitë matematike për vërtëtësinë e të cilave bindemi me anë të vërtetimit, quhen teorema”.

Çdo teoremë ka dy pjesë: kushtin dhe përfundimin.

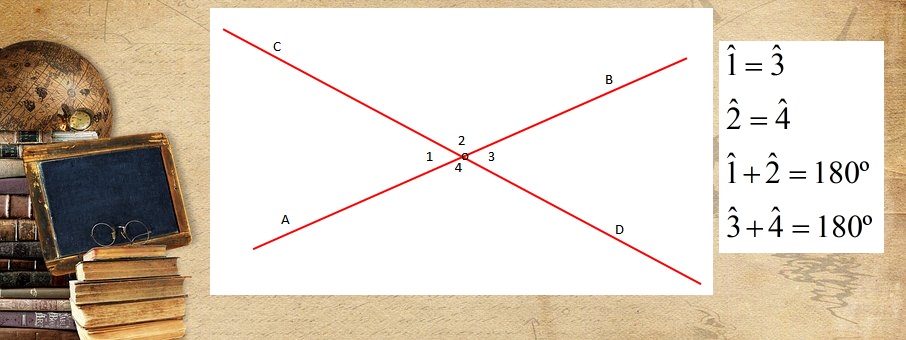
Kende te kundert ne kulm. Drejtëza pingule

Kende te kundert ne kulm

Përkufizim: “Dy kënde quhen të kundërt në kulm, nëse brinjët e njërit kënd janë gjysmëdrejtëza plotësuese të brinjëve të tjetrit”.

Teoremë: “Nëse dy kënde janë të kundërt në kulm, atëherë ata kanë masa të barabarta”.

Drejtëza pingule

Përkufizim: “Dy drejtëza prerëse quhen pingule, nëse njëri nga këndet që ato formojnë është i drejt”.

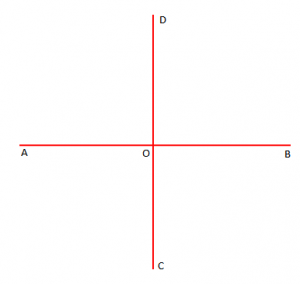
Teoremë: “Dy drejtëza pingule me një të tretë nuk priten”.

Ushtrimi 1

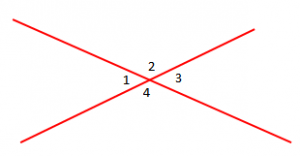
Në figurën më sipër, gjeni kendet 1, 2, 3, 4, nëse:

a) $\displaystyle \hat{2}+\hat{4}={{120}^{\text{o}}}$

b) $\displaystyle \hat{1}+\hat{3}=\hat{2}+\hat{4}$

c) $\displaystyle \hat{2}-\hat{1}=40{}^\text{o}$

Zgjidhje

a) $\displaystyle \hat{2}+\hat{4}={{120}^{\text{o}}}$

Dimë që kendet e kundërt në kulm janë të barabartë, ndaj do të kemi:

$\displaystyle \hat{2}=\hat{4}$

E shënojmë me x njërin kënd, dhe formojmë ekuacionin:

$\displaystyle x+x=120$

$\displaystyle 2x=120$

$\displaystyle x=60$

Pra, $\displaystyle \hat{2}=\hat{4}=60{}^\text{o}$

Tani gjejmë $\displaystyle \hat{1}$ dhe $\displaystyle \hat{3}$ .

Dimë që:

$\displaystyle \hat{2}+\hat{3}=180{}^\text{o}$

Shënojmë me x këndin 3 dhe formojmë ekuacionin:

$\displaystyle 60+x=180$

$\displaystyle x=180-60$

$\displaystyle x=120$

Pra, $\displaystyle \hat{1}=\hat{3}=120{}^\text{o}$ .

b) $\displaystyle \hat{1}+\hat{3}=\hat{2}+\hat{4}$

Nga këndet e kundërt në kulm, dimë që:

$\displaystyle \hat{1}+\hat{2}+\hat{3}+\hat{4}=360{}^\text{o}$

Meqë të gjitha këndet janë të barabarta, e shenojmë me x dhe formojmë ekuacionin:

$\displaystyle x+x+x+x=360$

$\displaystyle 4x=360$

$\displaystyle x=90$

Pra, $\displaystyle \hat{1}=\hat{2}=\hat{3}=\hat{4}=90{}^\text{o}$

c) $\displaystyle \hat{2}-\hat{1}=40{}^\text{o}$

$\displaystyle \hat{1}$ dhe $\displaystyle \hat{2}$ janë kënde shtues, ndaj do të kemi:

$\displaystyle \hat{1}+\hat{2}={{180}^{\text{o}}}$

Në fillimin shënojmë me x këndin 2 dhe do të kemi:

$\displaystyle \hat{2}=x$

$\displaystyle \hat{1}=x-40$

Tani $\displaystyle \hat{1}$ e zëvëndësojmë tek ekuacioni:

$\displaystyle \hat{1}+\hat{2}=180$

$\displaystyle \left( x-40 \right)+x=180$

$\displaystyle 2x-40=180$

$\displaystyle 2x=220$

$\displaystyle x=\frac{220}{2}$

$\displaystyle x={{110}^{\circ }}$

Pra, $\displaystyle \hat{2}={{110}^{\circ }}$

$\displaystyle \hat{1}={{110}^{\circ }}-{{40}^{\circ }}={{70}^{\circ }}$