Ushtrime te zgjidhura mbi siperfaqen e figurave | Matematika 7

Para se te zgjidhni ushtrimet me siperfaqen e figurave, ju duhet te lexoni Siperfaqja e figurave

Ushtrimi 1

Njehso katrorin e rrezes së një qarku me sipërfaqe $\displaystyle 113.04c{{m}^{2}}$

Zgjidhje

Dimë që:

$\displaystyle S=\pi \cdot {{r}^{2}}$

Atëherë:

$\displaystyle {{r}^{2}}=\frac{S}{\pi }$

$\displaystyle {{r}^{2}}=\frac{113.04}{3.14}=36$

Ushtrimi 2

Një rreth e ka perimetrin 62.8 cm. Njehsoni siperfaqen e rrethit.

Zgjidhje

Dimë që:

P = 2 ∙ π ∙ r

P = 62.8

2 ∙ π ∙ r = 62.8

$\displaystyle r=\frac{62.8}{2\pi }=\frac{31.4}{3.14}=10cm$

Atëherë:

$\displaystyle S=\pi \cdot {{r}^{2}}$

$\displaystyle S=\pi \cdot {{10}^{2}}=3.14\cdot 100$

$\displaystyle S=314c{{m}^{2}}$

Ushtrimi 3

Njehsoni siperfaqen e paralelogramit me të dhënat e figurave:

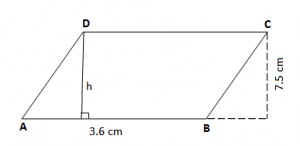
Në figurë kemi të dhënë:

[AB] = 3.6 cm = b

h = 7.5 cm

S = b ∙ h

$\displaystyle S=3.6\cdot 7.5=27c{{m}^{2}}$

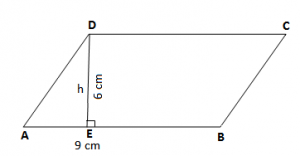
Në këtë figurë kemi të dhënë:

h = 6 cm.

[AB] = 9 cm = b

Atëherë kemi:

$\displaystyle S=b\cdot h=9\cdot 6=54c{{m}^{2}}$

Ushtrimi 4

Në një paralelogram, lartësia është sa $\displaystyle \frac{5}{8}$ e bazës me gjatësi 24 cm.

Njëhsoni siperfaqen e tij.

Zgjidhje

$\displaystyle h=\frac{5}{8}b$

$\displaystyle h=\frac{5}{8}\cdot 24=5\cdot 3=15cm$

Atëhere do të kemi:

$\displaystyle S=b\cdot h=24\cdot 15=360c{{m}^{2}}$

Ushtrimi 5

Në një parallelogram, njëra bazë është 5 cm dhe tjetra sa $\displaystyle \frac{2}{3}$ e lartësisë.

a) Gjeni siperfaqen e paralelogramit, duke ditur që lartësia e tij është 15 cm.

b) Gjeni perimetrin e paralelogramit.

Zgjidhje

a) Dimë që:

a = 3 cm

$\displaystyle b=\frac{3}{5}15=3\cdot 3=9cm$

h = 15 cm.

$\displaystyle S=b\cdot h=9\cdot 15=135c{{m}^{2}}$

b) Dimë që:

P = 2 ∙ (a + b) = 2 ∙ (3 + 9) = 24 cm

Ushtrimi 6

Në një parallelogram, baza është $\displaystyle \frac{4}{7}$ e lartësisë dhe sipërfaqja $\displaystyle 3388c{{m}^{2}}$ .

Njëhsoni siperfaqen e drejtkëndëshit që ka bazë të njëjtë me të dhe perimetër 158 cm.

Zgjidhje

Kemi të dhëna:

$\displaystyle b=\frac{4}{7}h$

$\displaystyle S=3388c{{m}^{2}}$

$\displaystyle {{P}_{d}}=158cm$

$\displaystyle {{b}_{d}}={{b}_{p}}$

Atëherë:

$\displaystyle {{S}_{p}}=\left( \frac{4}{7}h\cdot h \right)=3388$

$\displaystyle \frac{4{{h}^{2}}}{7}=3388$

$\displaystyle {{h}^{2}}=\frac{3388\cdot 7}{4}$

$\displaystyle {{h}^{2}}=5929$

$\displaystyle h=\sqrt{5929}$

$\displaystyle h=77cm$

Tani që gjetëm lartësinë e paralelogramit, gjejmë dhe bazën e drejtkëndëshit:

$\displaystyle {{b}_{d}}={{b}_{p}}=\frac{4}{7}h$

$\displaystyle {{b}_{d}}=\frac{4}{7}\cdot 77=4\cdot 11=44cm$

Dimë që perimetri i drejtkëndëshit është 158 cm, nga kjo gjejmë brinjën tjetër të drejtkëndëshit:

P = 2 ∙ (a + b)

158 = 2 ∙ a + 2 ∙ 11

$\displaystyle a=\frac{158-22}{2}=\frac{136}{2}$

$\displaystyle a=68cm$

Tani gjejmë siperfaqen e drejtkëndëshit:

$\displaystyle S=a\cdot b=11\cdot 68$

$\displaystyle S=748c{{m}^{2}}$

Ushtrimi 7

Diagonalet e paralelogramit priten në një pikë, largësia e së cilës nga baza është 10 cm. Baza është 85 cm.

Njëhsoni gjysmën e sipërfaqes së paralelogramit.

Zgjidhje

Ndërtojmë figurën:

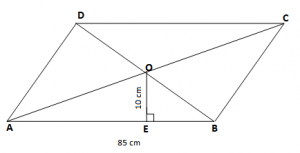
Kemi:

AB = 85 cm

OE = 10 cm

$\displaystyle OE\bot AB$

Nga vetitë eparalelogramit, ne dimë që: “Diagonalet e ndajnë paralelogramin në katër trekëndësha, dy nga dy kongruent”, pra:

∆AOB≡∆DOC

Rrjedhimisht, nësë do të ndërtonim lartësin OF mbi ∆DOC, do të kishim:

OE=OF=10 cm.
EF=10 + 10 = 20 cm.

Në paralelogramin ABCD, EF është lartësia e paralelogramit, ndaj gjejmë siperfaqen e plotë të paralelogramit:

S = b ∙ h = 85 ∙ 10

$\displaystyle S=850c{{m}^{2}}$

Për të gjetur gjysmën e sipërfaqes së paralelogramit, pjestojmë me 2 siperfaqen e plotë:

$\displaystyle {{S}_{\frac{1}{2}}}=\frac{S}{2}=\frac{850}{2}=425c{{m}^{2}}$

Ushtrimi 8

Në një trapez janë dhënë baza e madhe 20 cm dhe baza e vogel 12 cm.

Gjeni siperfaqen e trapezit, nëse lartësia e tij është 8 cm.

Zgjidhje

Kemi të dhënë:

B = 20 cm

b = 12 cm

h = 8 cm

Atëherë:

$\displaystyle S=\frac{\left( B+b \right)\cdot h}{2}$

$\displaystyle S=\frac{\left( 20+12 \right)\cdot {{{}}^{4}}}{{{{}}^{1}}}=32\cdot 4$

$\displaystyle S=128c{{m}^{2}}$

Ushtrimi 9

Gjeni siperfaqen e trapezit me të dhënat si në figurë:

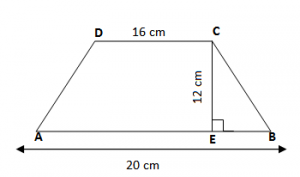
Kemi të dhënë:

AB = 20 cm

CD = 16

CE = 12 cm

Atëherë:

$\displaystyle S=\frac{\left( 20+16 \right)\cdot 12}{2}$

$\displaystyle S=36\cdot 6=216c{{m}^{2}}$

Ushtrimi 10

Në një trapez sipërfaqja e tij është $\displaystyle 1560c{{m}^{2}}$ dhe lartësia 24 cm.

Gjeni bazën e vogël të trapezit, nësë baza e madhe e tij është 80 cm.

Zgjidhje

$\displaystyle S=\frac{\left( B+b \right)\cdot h}{2}$

$\displaystyle B+b=\frac{2\cdot S}{h}$

$\displaystyle b=\frac{2\cdot S}{h}-B$

$\displaystyle b=\frac{2\cdot 1560}{24}-80$

$\displaystyle b=130-80=50cm$

Përgjigje: Baza e vogël e trapezit është 50 cm.

Ushtrimi 1

Zgjidhje

Ushtrimi 2

Një rreth e ka perimetrin 62.8 cm. Njehsoni siperfaqen e rrethit.

Zgjidhje

Ushtrimi 3

Ushtrimi 4

Zgjidhje

Ushtrimi 5

Zgjidhje

Ushtrimi 6

Zgjidhje

Ushtrimi 7

Zgjidhje

Ushtrimi 8

Zgjidhje

Ushtrimi 9

Ushtrimi 10

Zgjidhje

Postime te ngjashme: