Vektor quhet segmenti në të cilin njëri prej skajeve merret si origjinë (fillesë) dhe tjetri si ekstremitet (mbaresë)

Vektori me fillesë A dhe mbaresë në B paraqitet gjeometrikisht me anën e një shigjete dhe shënohet .

Kjo është paraqitje gjeometrike e vektorit AB.

Vektoret zakonisht shkruhen me një shkronjë të vetme, psh , , etj.

Gjatësi e vektorit quhet gjatësia e segmentit të tij dhe shënohet . Në rastin kur fillesa dhe mbaresa e vektorit përputhen, atëherë vektori quhet vektor-zero.

Vektoret bashkëvizorë

Përkufizim: “Vektoret që shtrihen në të njëjtën drejtëz apo në drejtëza paralele quhen vektorë bashkëvizorë (kolinearë)”.

Këta vektorë gjithashtu kanë dhe drejtim të njëjtë.

Dy vektorë bashkëvizorë kanë kahe të njëjta, nëse mbaresat e tyre janë në të njëjtën anë të drejtëzës që bashkon fillesat e tyre.

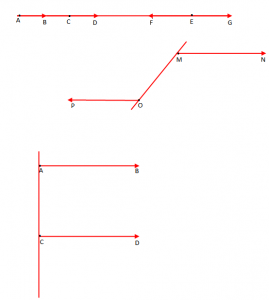
Këta janë disa vektorë bashkevizorë.

Vektoret dhe janë vektorë me kahe të njëjta.

Barazimi i vektorëve

Përkufizim: “Dy vektorë quhen të barabartë nëse kanë drejtim të njëjtë, kah të njëjtë dhe gjatësi të njëjtë”.
Nëse vektoret dhe janë të barabartë, shkruajmë:

.

Nga barazimi rrjedh barazimi i gjatësive AB = CD, por e anasjellta nuk është teoremë. Pra, nga barazimi i gjatësive të dy vektorëve nuk rrjedh detyrimisht që vektoret janë të barabartë.

Përkufizim: “Dy vektorë quhen të kundërt kur kanë drejtim të njëjtë, gjatësi të njëjtë, por kahe të kundërta”.

Kur vektorët dhe janë të kundërt shkruajmë:

.

Zhvendosja e vektorit në një pikë të dhënë

Të zhvendosësh vektorin në pikën O do të thotë të ndërtosh një vektor të barabartë me , por me fillesë në pikën O.

Për ta bërë këtë, heqim nga pika O një drejtëz që është paralele me AB. Në drejtëzën e ndërtuar marrim, në kahun e vektorit , një pikë P, të tillë që OP=AB. Do të kemi .

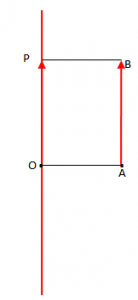
Kjo është zhvendosja e vektorit në pikën O.