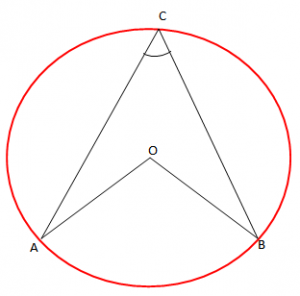
Kendi rrethor

Rrethin e kemi mësuar më herët dhe këtu kemi disa pika të rëndësishme per të rikujtuar:

Rreth quhet figura gjeometrike e përbërë nga të gjitha pikat e planit që kanë të njëjtën largesë nga një pikë fikse e dhënë. Kjo largesë quhet rreze e rrethit.
Drejtëza e hequr nëpër një pikë të rrethit, pingule me rrezen që kalon nëpër këtë pikë të rrethit, quhet tangjente e rrethit.
Këndi me kulm në qëndrën e rrethit quhet kënd qëndror. Masa në gradë e këndit qëndror është e njëjtë me masën në gradë të harkut më të vogël që ai pret në rreth.

Përkufizim: “Këndi me kulm në rreth, brinjët e të cilit presin rrethin quhet kënd rrethor”.

Këndi $\displaystyle A\hat{C}B$ e ka kulmin në rreth. Ky është kendi rrethor.

Teoremë: “Masa e këndit rrethor është e barabartë me gjysmën e masës së këndit qëndror përgjegjës”.

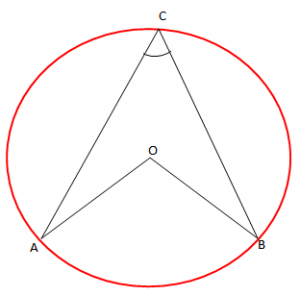
Pra, $\displaystyle A\hat{C}B=\frac{1}{2}A\hat{O}B$ .

Teorema mund të formulohet edhe kështu: “Masa e këndit rrethor është sa gjysma e masës së harkut në të cilin ai mbështetet”.

Ushtrimi 1

Këndi qëndror është 40º më i madh se kendi rrethor që mbështetet në të njëtin hark. Gjeni secilin nga këto kënde.

Zgjidhje

Nga teorema, dimë që: “Masa e këndit rrethor është sa gjysma e masës së harkut në të cilin ai mbështetet”, ndaj shkruajmë:

Këndin rrethor e shënojmë me $\displaystyle \hat{A}$ , ndërsa këndin qëndror e shënojmë me $\displaystyle \hat{B}$ dhe do të kemi:

$\displaystyle \hat{A}=\frac{1}{2}\hat{B}$ .

Gjithashtu kemi:

$\displaystyle \hat{B}=40+\hat{A}$

Bëjmë zëvëndësimet tek ekuacioni i parë:

$\displaystyle \hat{A}=\frac{1}{2}\left( 40+\hat{A} \right)$

$\displaystyle \hat{A}=20+\frac{{\hat{A}}}{2}$

$\displaystyle 2\hat{A}=40+\hat{A}$

$\displaystyle \hat{A}=40{}^\text{o}$

Tani gjejmë $\displaystyle {\hat{B}}$ :

$\displaystyle \hat{B}=2\cdot 40{}^\text{o}=80{}^\text{o}$

Zbatime të këndit rrethor

Këndët rrethor që mbështeten në të njëjtin hark

Teoremë: “Të gjithë këndet rrethor që mbështeten në të njëjtin hark, kanë masa të barabarta”.

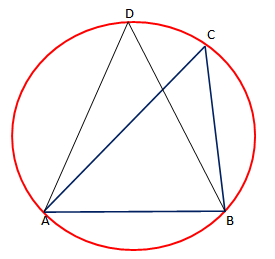
Pra, $\displaystyle A\hat{C}B=A\hat{D}B$

Rast i veçantë: “Kendi rrethor që mbështetet mbi gjysmën e rrethit është i drejtë”.

Harqet që priten në rreth nga dy korda paralele

Teoremë: “Dy korda paralele të një rrethi presin në të dy harqe me masa të barabarta”.

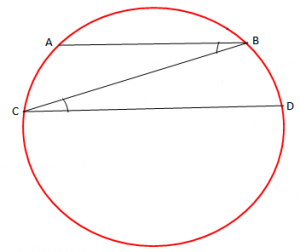
Pra, harku A është i barabartë me harkub B.