
Siperfaqja e drejtkendeshit dhe trekendeshit
Ne dimë që siperfaqja e drejtkendeshit është e barabartë me prodhimin e përmasave të tij.
Sipërfaqja e katrorit është e barabartë me katrorit e përmasës së tij.
Sipërfaqja e trekëndëshit është e barabartë me gysmën e prodhimit të një brinje me lartësinë e hequr mbi të.
Kemi rastet e ilustruara me figurë:
- Siperfaqia e Drejtkendeshit
- Siperfaqia e Katrorit
- Siperfaqia e Trekendeshit
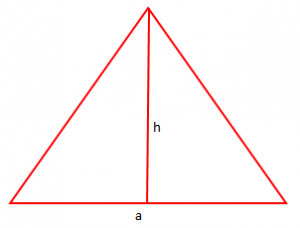
Shembull 1
Gjeni sipërfaqen e trekëndëshit dybrinjëshëm me gjatësi të bazës 16 cm dhe brinjë anësore 10 cm.
Zgjidhje
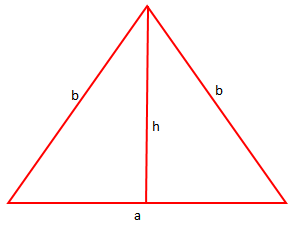
Kemi:
a = 16 cm
b = 10 cm.
Në fillim gjejmë lartësinë e trekëndëshit me ndihmën e teoremës së pitagorës:
Tani gjejmë sipërfaqen e trekëndëshit:
Siperfaqja e paralelogramit
Teoremë: “Siperfaqja e paralelogramit është e barabartë me prodhimin e bazës me lartësinë”.

Pra,
Siperfaqja e trapezit
Teoremë: “Siperfaqja e trapezit është e barabartë me gjysmën e prodhimit të shumës së bazave me lartësinë”.

Pra, .
Shembull 1
Gjeni sipërfaqen e trapezit me shumë brinjësh 26 cm dhe lartësi 12 cm.
Zgjidhje
Kemi:
b+B = 26 cm
h = 12 cm
Nga formula, dimë që:
Bëjmë zëvëndësimet:
Zbatime
Teoremë 1: “Raporti i sipërfaqeve të dy trekëndëshave me lartësi të barabartë është i barabartë me raportin e bazave të tyre”.
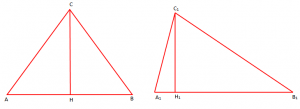
Pra, Nëse , do të kemi:
Teoremë 2: “Raporti i sipërfaqeve të dy trekëndëshave që kanë një kënd të barabartë është i barabartë me raportin e prodhimit të brinjëve që formojnë këtë kënd”.
Pra, nëse , do të kemi:
.


