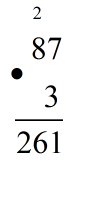Shumezimi është mbledhja me mbledhorë të barabartë. Për shembull: 5 + 5 + 5 +5 + 5 + 5 = 30 (Tabelen e shumezimit e kemi trajtuar ketu)
Pra, shuma e gjashtë pesave jep numrin 30, e cila është njësoj nëse ne e shkruajmë 5 ∙ 6 = 30
Gjithashtu mund të themi se kur shumëzojmë dy numra përfitojmë një shumfish të përbashkët të tyre. Konkretisht në këtë rast shumëfishi i përbashkët i numrit 30 është përkatësisht numri 5 dhe 6:
Rezultati që del nga shumezimi i dy numrave do ta quajmë ndryshe prodhim.
Ne kemi mësuar disa veti të shumezimit . Për shembull:
Vizatojmë një rrjet katrorësh 6 ∙ 6 dhe vendosim numrat nga 2-6:
∙ |
2 | 3 | 4 | 5 |
6 |
|
2 |
4 | 6 | 8 | 10 | 12 |
|
3 |
6 | 9 | 12 | 15 |
18 |
|
4 |
8 | 12 | 16 | 20 |
24 |
|
5 |
10 | 15 | 20 | 25 |
30 |
|
6 |
12 | 18 | 24 | 30 |
36 |
Mënyra se si kemi vepruar në plotësimin e tabelës është :
2 ∙ 2 = 4 (shprehet si shumë e dy dyshave 2+2 =4 )
2 ∙ 3 = 6 ( shprehet si shumë e dy treshave 3 +3 = 6 )
2 ∙ 4 = 8 ( shprehet si shumë e dy katrave 4+ 4 = 8 )
2 ∙ 5 = 10 ( shprehet si shumë e dy pesave 5+ 5= 10 )
2 ∙ 6 = 12 ( shprehet si shumë e dy gjashtave, pra 6 + 6 = 12 )
Pasi mbaruam me numrin 2, kalojmë me numrin 3, i cili shumëzon të gjithë numrat me ngjyrë blu horizontalisht dhee kështu me radhë vazhdojmë deri tek numri 6:
3 ∙ 2 = 6
3 ∙ 3 = 9
3 ∙ 4 = 12
3 ∙ 5 = 15
3 ∙ 6 = 18
Në mënyrë të ngjashme kryhet edhe me numrat e tjerë në vazhdimësi…
Ushtrimi 1
Shkruaj 5 shumëfishat e parë të katrës.
Zgjidhje:
4 ∙ 1 = 4
4 ∙ 2 = 8
4 ∙ 3 = 12
4 ∙ 4 = 16
4 ∙ 5 = 20
Ushtrimi 2
Shkruaj shumëfishat e 6-ës më të vegjel se 40.
Zgjidhje:
6 ∙ 1 = 6
6 ∙ 2 = 12
6 ∙ 3 = 18
6 ∙ 4 = 24
6 ∙ 5 = 30
6 ∙ 6 = 36
6 ∙ 7 = 42
6 ∙ 8 = 48
………………..
Shumëfishat e 6-s me të vegjel se 40 janë 6, 12, 18, 24, 30 dhe 36,. Pasi veprimi i numrave që janë me të kuqe edhe pse janë shumëfishat e 6-s ata nuk i përmbahen kërkesës së ushtrimit tonë pasi janë më të mëdhej se 40.
Ushtrimi 3
Janë dhënë 3 simbole dhe 3 shumëzime ku janë përdorur ato.
Zbuloni secilin prej simboleve:
a) 2 • ◊ = 8.
Sa është ai numër që po ta shumëzojmë me 2 jep rezultatin 8?
Le t`i marrim me radhë:
2 ∙ 1 = 2
2 ∙ 2 = 4
2∙ 3 = 6
2∙ 4 = 8
Në varësi të shumëzimeve që ne kryem pamë që numri në të cilën shumëzohet me 2 dhe jep rezultatin 8 është numri 4. Pra simboli ◊ = 4 .
b) ◊ · O = 12
Duke qënë se ◊ = 4 , e zëvendësojmë tek barazimi më lart dhe kemi:
4 ∙ O = 12. Kryejmë shumëzimet me radhë:
4 ∙ 1 = 4
4 ∙ 2 = 8
4 ∙ 3 = 12 Pra, vëmë re se numri 3 është pikërisht ai numër që po t’a shumëzojmë me 4 jep rezultatin 12.
Përgjigje: Simboli O = 3.
c) O ∙ Δ = 24
O ∙ Δ = 24 ( O = 3, e zëvendësojmë dhe kemi):
3 ∙ Δ = 24 ( në mënyrë të ngjashme si vepruam më lart, arrijmë të gjejmë se numri me të cilën e shumëzojme me 3 dhe jep rezultatin 24 është numri 8. Pra simboli Δ = 8.
3 ∙ 8 = 24
Përgjigje: Zbuluam se ◊ = 4 , O = 3 , Δ = 8.
Ushtrimi 4
Kryeni veprimet duke përdorur tabelën:
Disa mënyra për të shumëzuar numra dyshifrorë.
Jepet tabela :
∙ |
2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
10 |
|
2 |
4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
20 |
|
3 |
6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 |
30 |
|
4 |
8 | 12 | 16 | 20 | 2 4 | 28 | 28 | 36 |
40 |
|
5 |
10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
50 |
|
6 |
12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 |
60 |
|
7 |
14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 |
70 |
|
8 |
16 | 24 | 28 | 40 | 48 | 56 | 64 | 72 |
80 |
Le të bazohemi tek tabela për të kryer shumëzime me numra të mëdhenjë.
Marrim:
2 ∙ 2 = 4
10 ∙ 2= 20
Kështu që 12 ∙ 2 = 24 ( e cila del si rezultat ( 10 + 2 ) ∙ 2 = ( 20 + 4)
3 ∙ 3 = 9
10 ∙ 3 = 30
Kështu që 13 ∙ 3 = 39. [sepse 3+ 10 ) ∙ 3 = (9 +30 )]
2 ∙ 4 = 8
5 ∙ 4 = 20
10 ∙ 4 = 40
Kështu që 17 ∙ 4 = 68 [sepse ( 2 + 5 + 10 ) ∙ 4 = ( 8+ 20+ 40 )]
Ushtrimi 5
Kryeni veprimet duke shikuar tabelën :
a) 16 ∙ 3
b) 17 ∙ 6
c) 15 ∙ 9
Zgjidhje:
a) 16 ∙ 3
16 e shkruajmë si zbërthim faktorësh, pra:
16 = ( 10 + 6 )
Do të kemi:
6 ∙ 3 = 18
10 ∙ 3 = 30
Përgjigje: 16 ∙ 3 = 48, pra 30+18
b) 17 ∙ 6
17 e shkruajmë si zbërthim faktorësh:
17 = (10+7)
Do të kemi:
7 ∙ 6 = 42
10 ∙ 6 = 60
Përgjigje: 1 7 ∙ 6 = 102, pra 60+ 42.
c) 15 ∙ 9
15 e shkruajmë si zbërthim faktorësh
(10 +5 ), do të kemi:
5 ∙ 6 = 30
10 ∙ 6 = 60
Përgjigje: 15 ∙ 6 = 90
Shumezimi dhe pjesëtimi me 10, 100 , 1000
Shumezimi
Jepet tabela :
|
Dh.mijëshe |
Mijëshe | Qindëshe | Dhjetëshe |
Njëshe |
| 3 |
8 |
|||
| 3 | 8 |
0 |
||
| 3 | 8 | 0 |
0 |
|
| 3 | 8 | 0 | 0 |
0 |
Le ta shpjegojmë se si kryhet shumezimi me 10 , 100 , 1000 duke shikuar tabelën:
Kemi numrin 38 dyshifror, e shprehim atë në formë të zbërthyer si 30 + 8.
– Në rastin kur shumëzojmë 38 ∙ 10, zhvendosim në tabelë shifrën 38 një kuti majtas dhe vendosim zero nëzi vendet e mbetura bosh nga ana e djathtë. Pra, 38 ∙ 10 = 380
– Në rastin kur shumëzojme 38 ∙100, zhvendosim në tabelë shifrën 38 dy kuti dhe vendosim zero në vendet e mbetura bosh. Pra, do të kemi: 38 ∙ 100 = 3800
– Në rastin kur shumëzojmë 38 ∙ 1000, zhvendosim në tabelë shifrat 3 kuti majtas dhe vendosim me zero në kutitë që na mbeten. Pra, do të kemi: 38 ∙ 1000 = 38 000.
Pjesëtimi
Në të njëjtën mënyrë shpjegojmë dhe mbi pjesetimin duke e ilustruar me anë të tabelës.
Ndërtojmë tabelën :
|
Dhjetëshe |
Njëshe | , |
Të dhjeta ( 1/ 10 ) |
|
9 |
2 | , | |
| 9 | , |
2 |
-Kur pjestojmë me 10, shifrat lëvizin nga e majta në të djathë , duke e zhvendosur në një rend 10 herë më të vogël. 92 : 10 = 9 ,2
|
Qindëshe |
Dhjetëshe | Njëshe | , | Të dhjeta (1.10) | Të qindëta (1/100) |
|
1 |
4 | 5 | , | ||
| 1 | , | 4 |
5 |
– Kur pjestojmë me 100 , shifrat lëvizin nga e majta në të djathë dy kuti në një rend 100 herë më të vogël . Pra. do të kemi: 145 : 100 = 1, 45.
Në të njëjtën mënyrë veprojmë edhe kur pjestojmë me 1000 , duke lëvizur shifrat nga e majta në të djathe me 3 kuti . Me një rend 1000 më të vogël. Pë shembull: 2548 : 1000 = 2, 548
Ushtrimi 1
Kryeni veprimet me mend. Shkruani vetëm përgjigjet.
a) 123 ∙ 10 = 1’230
15 ∙ 100 = 1’500
6770 ∙ 1000 = 6’770’000
b) 29: 10 = 2.9
153: 100 =1.53
1: 1000 = 0.001
Mënyra të ndryshme për shumezimin dhe pjesetimin e numrave natyrorë
Kemi mësuar se si të shumëzojmë dhe të pjestojmë një numër natyror duke e shumëzuar dhe pjestuar atë me numrat 10, 100 , 1000. Gjithashtu mësuam se si bëhet shumezimi i dy numra 2-shifërorë.
Le të njihemi me një nga menyrat më të thjeshta për kryerjen e shumëzimit të dy numrave natyrorë:
Ushtrimi 1
a) Kemi prodhimin: 877 ∙ 3
Mënyra e parë:
Hapi që ndjekim eshte: e ndajmë numrin 877 si zbërthim faktoresh:
= ( 800 + 70 + 7 ) ∙ 3 ( kryejmë shumezimin e cdo numri që ndodhet brenda kllapës me 3 )
= (800 ∙ 3 ) + (70 ∙ 3 ) +( 7 ∙ 3 )
= 2400 + 210 + 21
= 2631
Mënyra e dytë:
b) Kemi prodhimin 128 ∙ 8
( në mënyrë të ngjashme zgjidhim dhe piken b)
= (100 + 20 +8 ) ∙ 8
= (100 ∙ 8) + ( 20 ∙ 8 ) + ( 8 ∙ 8 )
= 800 + 160 + 64
= 1024
Mënyra e dytë:
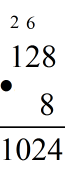
Ushtrimi 2
Kryej shumezimet me mënyrën më të thjeshtë.
Shumezimi:
- Shumezimi
- Herë më shumë
- Prodhimi
- Prodhimi i…..
- Dyfishi , trefishi
- Sa herë më e gjatë
Të gjitha këto fjalë nëse përdorën nëpër ushtrime ne nënkuptojmë se kryerja e veprimeve do të jetë shumezimi.
Pjesëtimi:
- Ndaj , pjesto
- Sa grupe formohen
- Gjysma , cereku
- Sa janë në mënyrë të barabartë
- Ndaj në mënyrë të barabartë
Të gjitha keto fjalë nënkuptojmë se kryerja e veprimeve do të jetë me pjesetim.
Problema me shumëzim dhe pjesëtim
Problema 1
Një libër ushtrimesh ka 115 faqe. Sa faqe kanë 4 libra ushtrimesh ?
Zgjidhje:
Të dhënat:
1 libër -> 115 faqe
4 libra -> ?
4 libra ∙ 115 faqe që ka secili libër.
= 4 ∙ (100 + 10 + 5 )
= ( 4 ∙ 100 ) +( 4 ∙ 10 ) + ( 4 ∙ 5 )
= 400 + 40 + 20
= 460 faqe.
Përgjigje: 460 faqe.
Problema 2
Eduarti paketoi 80 ëmbëlsira në kuti që nxënë nga 5 copë secila. Sa kuti i duhen atij?
Të dhënat:
80 ëmbëlsira.
5 copë çdo kuti.
80:5 = 16 kuti.
Përgjigje: Eduartit i duhen 16 kuti.
Problema 3
Juli ka marrë me vete për në shkollë 78 lekë. Andi ka 12 herë më shumë .
a) Sa lekë ka Andi?
Kur themi “herë” e nënkuptojmë shumezimi .
Duke qënë se Andi ka 12 herë më shumë se Juli . Kemi :
12 ∙ 78 = 936
Përgjigje: 936 lekë ka marrë me vete Andi.
b) Sa lekë kanë së bashku?
78 lekë Juli + 936 lekë Andi = 1014 lekë.
Përgjigje: lekë kanë ata gjithësej
Problema 4
Eduatri paketoi 80 ëmbëlsira në kuti që nxënë nga 5 copë secila. Sa kuti i duhen atij ?
Zgjidhje:
Në këtë rast kemi të bëjmë me pjesëtim:
1 kuti = 5 copë.
80 ëmbëlsira : 5 copë secila = 40 kuti.
Përgjigje: 40 kuti i duhen atij.
Problema 5
54 nxënës së klasës së 6 –të do të blejnë 15 lapsa secili. Sa lapsa kanë blerë së bashku?
Zgjidhje:
1 nxënës = 15 lapsa.
54 nxënës = ?
54 nxënës ∙ 15 lapsa që bleu secili = 810 lapsa.
Përgjigje: 810 lapsa kanë blerë së bashku .
Problema 6
Një shitëse shet 588 kg mollë në javë . Sa kg shet ajo në ditë ?
Zgjidhje:
588 kg mollë në javë
Një javë është e përbërë nga 7 ditë
Kemi 588 : 7 = 84 kg
Përgjigje: 84 kg mollë shet ajo në ditë
Problema 7
Një shkollë mbledh para për bamirësi . Këtë muaj ajo mblodhi 3 herë më shumë se muajin e kaluar. Muajin e kaluar ajo mblodhi 34 000 lekë.
a) Sa lekë mblodhi shkolla këtë muaj?
b) Sa lekë mblodhi shkolla për bamirësi në të dy muajt sa bashku ?
Zgjidhje:
Të dhënat:
- 34 000 lekë mblodhën muajin e kaluar
- Këtë muaj 3 herë më shumë se muajin e kaluar
a) 3 ∙ 34 000 = 102’000
Përgjigje: 102’000 lekë mblodhën këtë muaj.
b) Muajin e parë mblodhën 34 000 lekë.
Muajin e dytë mblodhën 102’000 lekë.
Në të dy muajt do të kemi 34’000 + 102’000 = 136’000 lekë.
Përgjigje: 136’000 lekë kanë mbledhur në të dy muajt së bashku.