Binomi i fuqise se pare me nje ndryshore | Matematika 10

Binomi i fuqisë së parë

Përkufizim 1: “Shprehja ax+b quhet binom i fuqisë së parë me një të panjohur”.

X është i panjohur, a dhe b janë numra realë, ku $\displaystyle a\ne 0$ .

Përkufizim 2: “Rrënjë të binomit ax+b do të quajmë rrënjën e ekuacionit ax+b=0”. Pra, rrënja e tij është $\displaystyle x=-\frac{b}{a}$ .

a është koeficienti para x, ndërsa b është term i lirë.

Studimi i shënjës së binomit ax+b

Pas faktorizimit të a-së tek binomi do të kemi: $\displaystyle ax+b=a\left( a+\frac{b}{a} \right)$ .

Rasti i parë: $\displaystyle x>-\frac{b}{a}\Leftrightarrow x+\frac{b}{a}>0$

Nëse $\displaystyle a>0\Leftrightarrow a\left( x+\frac{b}{a} \right)>0$ .

Nëse $\displaystyle a<0\Leftrightarrow a\left( x+\frac{b}{a} \right)<0$ . Rasti i dytë: $\displaystyle x<-\frac{b}{a}\Leftrightarrow x+\frac{b}{a}<0$ . Nëse $\displaystyle a>0\Leftrightarrow a\left( x+\frac{b}{a} \right)<0$ . Nëse $\displaystyle a<0\Leftrightarrow a\left( x+\frac{b}{a} \right)>0$ .

Rasti i tretë: $\displaystyle x=-\frac{b}{a}\Leftrightarrow x+\frac{b}{a}=0$

Për çdo vlerë të a-së $\displaystyle a\left( x+\frac{b}{a} \right)=0$ .

Përfundim: Për x më të mëdhenj se rrënja binomi ka shenjën e a-së, për x më të vegjël se rrënja binomi ka shenjën e kundërt të a-së, për x të barabartë me rrënjën binomi merr vlerën zero.

Ndërtojmë tabelën për studimin e shënjës së binomit:

Etapat që kalohen për studimin e shënjës së binomit janë:

Binomi barazohet me zero.
Zgjidhet ekuacioni i formuar
Ndërtohet tabela e studimit të shënjës.

Shembull 1

Të studiohet shenja e binomit $\displaystyle 2x-6$ .

Zgjidhje

Zgjidhim ekuacionin:

$\displaystyle 2x-6=0$

$\displaystyle 2x=6$

$\displaystyle x=3$

Ndërtojmë tabelën:

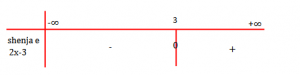
Nga tabela kuptojmë se për $\displaystyle x\in \left] -\infty ,3 \right[$ binomi ka vlera negative; për $\displaystyle x\in \left] 3,+\infty \right[$ merr vlera pozitive dhe për $\displaystyle x\in \left\{ 3 \right\}$ merr vlerën zero.

Shembull 2

Të studiohet binomi $\displaystyle 4-x$

Zgjidhje

Zgjidhim ekuacionin:

$\displaystyle 4-x=0$

$\displaystyle x=4$

Ndërtojmë tabelën:

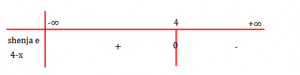
Nga tabela kuptojmë se për $\displaystyle x\in \left] -\infty ,4 \right[$ binomi ka vlera pozitive; për $\displaystyle x\in \left] 4,+\infty \right[$ merr vlera negative dhe për $\displaystyle x\in \left\{ 4 \right\}$ merr vlerën zero.

Shembull 3

Të studiohet shenja e binomit $\displaystyle 4x-16$

Zgjidhje

Zgjidhim ekuacionin:

$\displaystyle 4x-16=0$

$\displaystyle 4x=16$

$\displaystyle x=4$

Tani ndërtojmë tabelën për studimin e shenjës së binomit:

Nga tabela del se për $\displaystyle x\in \left] -\infty ,3 \right[$ binomi ka vlera negative, për $\displaystyle x\in \left] 3,+\infty \right[$ merr vlera pozitive dhe për $\displaystyle x\in \left\{ 3 \right\}$ merr vlerën zero.