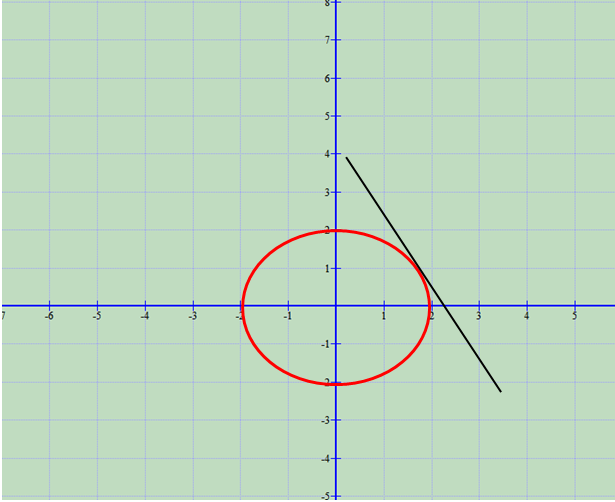
Ekuacioni i tangjentes dhe pingules se rrethit

Ekuacioni i tangjentes se rrethit

Kemi mësuar që ekuacioni i rrethit ka trajtën $\displaystyle {{\left( x-a \right)}^{2}}+{{\left( x-b \right)}^{2}}={{r}^{2}}$ .

Në këtë artikull do të trajtojmë shkurtimisht ekuacionin e tangjentes së rrethit.

Ekuacioni i tangjentes së rrethit shkruhet:

$\displaystyle x\cdot {{x}_{1}}+y\cdot {{y}_{1}}={{r}^{2}}$

Shembull 1

Jepet rrethi me ekuacion $\displaystyle {{x}^{2}}+{{y}^{2}}=25$ dhe pika $\displaystyle M\left( 3,4 \right)$ .

a) Të tregohet se pika M është pikë e rrethit.

b) Të shkruhet ekuacioni i tangjentes ndaj rrethit në pikën M.

Zgjidhje

a) Zëvëndësojmë koordinatat e pikës M në ekuacionin e rrethit. Do të kemi:

$\displaystyle {{3}^{2}}+{{4}^{2}}=25$

$\displaystyle 9+16=25$

$\displaystyle 25=25$ , pra pika M është pikë e rrethit.

b) Në ekuacionin e tangjentes zëvëndësojmë $\displaystyle {{x}_{1}}=3$ dhe $\displaystyle {{y}_{1}}=4$ . Do të kemi:

$\displaystyle x\cdot 3+y\cdot 4=25$

$\displaystyle 3x+4y-25=0$ .

Ekuacioni i pingules në një pikë të rrethit

Pingule ndaj rrethit në pikën M të tij, quhet drejtëza, e cila është pingule me tangjentën në këtë pikë. Nga vetia e tangjentes së rrethit, del se rrezja e rrethit është drejtëza pingule me tangjenten.

Meqë ajo kalon nga origjina e koordinatave, ekuacioni i saj është $\displaystyle y=kx$ , ku $\displaystyle k=\frac{{{y}_{1}}}{{{x}_{1}}}$ .

Pra, ekuacioni i pingules është:

$\displaystyle y=\frac{{{y}_{1}}}{{{x}_{1}}}\cdot x$ .

Shembull 2

Shkruani ekuacionin e tangjentes dhe të pingules së rrethit $\displaystyle {{x}^{2}}+{{y}^{2}}=5$ në pikën $\displaystyle M\left( 1,-2 \right)$ të tij.

Zgjidhje

Gjejmë ekuacionin e tangjentes së rrethit:

Në ekuacionin e tangjentes zëvëndësojmë $\displaystyle {{x}_{1}}=1$ dhe $\displaystyle {{y}_{1}}=-2$ . Do të kemi:

$\displaystyle x\cdot 1+y\cdot \left( -2 \right)=5$

$\displaystyle x-2y-5=0$

Gjejmë ekuacionin e pingules:

$\displaystyle y=\frac{{{y}_{1}}}{{{x}_{1}}}\cdot x$

$\displaystyle y=-2x$

$\displaystyle 2x+y=0$

Kushti i tangjencës së rrethit së drejtëzës me rrethit

Jepet rrethi $\displaystyle {{x}^{2}}+{{y}^{2}}={{r}^{2}}$ dhe drejtëza $\displaystyle y=kx$ .

Për të gjetur pikat e përbashkëta të tyre zgjidhim sistemin e ekuacioneve:

Duke zëvëndësuar y në ekuacionin e parë, kemi:

$\displaystyle {{x}^{2}}+{{\left( kx+t \right)}^{2}}={{r}^{2}}$

$\displaystyle {{x}^{2}}+{{k}^{2}}{{x}^{2}}+2ktx+{{t}^{2}}={{r}^{2}}$

$\displaystyle {{x}^{2}}\left( 1+{{k}^{2}} \right)+2ktx+\left( {{t}^{2}}-{{r}^{2}} \right)=0$

Në këtë rast përftohet një ekuacion i fuqisë së dytë me ndryshore x-in.

Dallori i thjeshtuar i këtij ekuacioni është $\displaystyle {{k}^{2}}{{x}^{2}}+{{r}^{2}}-{{t}^{2}}$ .

Dallojmë tre raste për dallorin:

$\displaystyle D<0$ . Në këtë rast ekuacioni nuk ka zgjidhje, pra drejtëza nuk e pret rrethin.
$\displaystyle D>0$ . Në këtë rast ekuacioni ka dy rrënjë, pra drejtëza e pret në dy pika rrethin.
$\displaystyle D=0$ .

$\displaystyle {{k}^{2}}{{r}^{2}}+{{r}^{2}}-{{t}^{2}}$ .
$\displaystyle {{k}^{2}}{{x}^{2}}+{{r}^{2}}={{t}^{2}}$ .

$\displaystyle {{r}^{2}}\left( {{k}^{2}}+1 \right)={{t}^{2}}$ .
Në këtë rast ekuacioni ka vetëm një rrenjë, pra drejtëza e pret vetëm në një pikë rrethin, pra drejtëza është tangjente me rrethin.

Në këtë mënyrë kemi gjetur kushtin që drejtëza $\displaystyle y=kx+t$ të jetë tangjente me rrethin $\displaystyle {{x}^{2}}+{{y}^{2}}={{r}^{2}}$ , ai është: