Variacioni i sinusit dhe kosinusit | Funksionet trigonometrike| Detyra.Al

Variacioni i sinusit

Marrin në rrethin trigonometrik harkun trigonometrik

*** QuickLaTeX cannot compile formula:
\displaystyle \overset\froën{AM}

*** Error message:
Invalid UTF-8 byte sequence (m@th).
leading text: $\displaystyle \overset\fro

me vlerë x. Për të parë se si ndryshon sinx, kur x rritet nga 0 në 2π, mjafton të shohim se si ndryshon ordinate e pikës M.

Kur $\displaystyle x=0$ , pika M puthitet me A. Kemi $\displaystyle {{y}_{M}}=0$ , pra $\displaystyle \sin 0=0$ .

Kur x rritet nga 0º në 90º (nga 0 në $\displaystyle \frac{\pi }{2}$ ), pika M lëviz në rrethin trigonometrik nga A në B. Ordinata e pikës M rritet, pra sinusi rritet.

Shohim figurën:

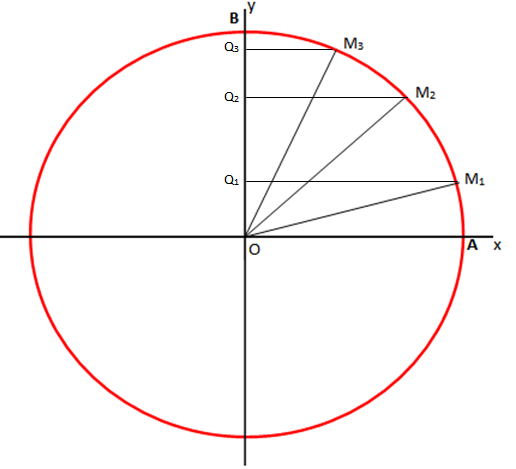
Gjatësitë e segmenteve [OQ₁], [OQ₂], [OQ₃] tregojnë vlerën e sinusit.

Nga figura duket qart që në $\displaystyle \left[ 0,\frac{\pi }{2} \right]$ , nga $\displaystyle {{x}_{2}}>{{x}_{1}}$ rrjedh $\displaystyle O{{Q}_{2}}>O{{Q}_{1}}$ .

Pra, $\displaystyle {{y}_{M2}}>{{Y}_{M1}}$ , dmth $\displaystyle \sin {{x}_{2}}>\sin {{x}_{1}}$ .

Kur pika $\displaystyle x=\frac{\pi }{2}$ , pika M puthitet me pikën B dhe $\displaystyle {{y}_{M}}=1$ . Pra, $\displaystyle \sin \left( \frac{\pi }{2} \right)=1$ .

Kur x rritet nga 90º në 180º (nga $\displaystyle \frac{\pi }{2}$ në $\displaystyle \pi$ ), pika M lëviz mbi rrethin trigonometrik nga B në A’. Ordinata e M zvogëlohet, pra sinusin zvogëlohet.

Shohim figurën:

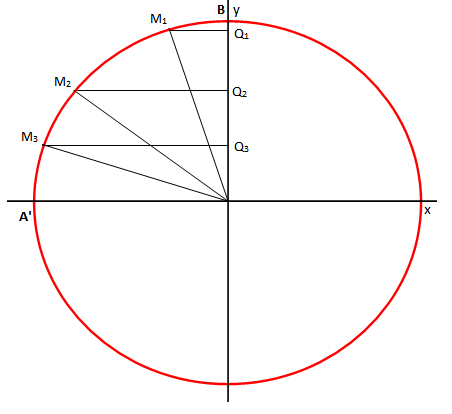
Nga figura duket qart se në $\displaystyle \left[ \frac{\pi }{2},\pi \right]$ , nga $\displaystyle {{x}_{2}}>{{x}_{1}}$ rrjedh $\displaystyle O{{Q}_{2}}<O{{Q}_{1}}$ . Pra, $\displaystyle {{y}_{M2}}<{{Y}_{M1}}$ , dmth $\displaystyle \sin {{x}_{2}}<\sin {{x}_{1}}$ . Kur $\displaystyle x=\pi$ , pika M puthitet me A’, prandaj $\displaystyle {{y}_{M}}=0$ , dmth $\displaystyle \sin \pi =0$ .

I njëjti arsyetim bëhet dhe për segmentet $\displaystyle \left[ \pi ,\frac{3\pi }{2} \right]$ (ku me rritjen e vlerave të x-it rritet dhe vlera e sinusit) dhe $\displaystyle \left[ \frac{3\pi }{2},2\pi \right]$ (ku me rritjen e vlerës së x-it ulet vlera e sinx). Në këto 2 segmente do të shohim dhe që $\displaystyle \sin \frac{3\pi }{2}=-1$ dhe $\displaystyle \sin 2\pi =0$ .

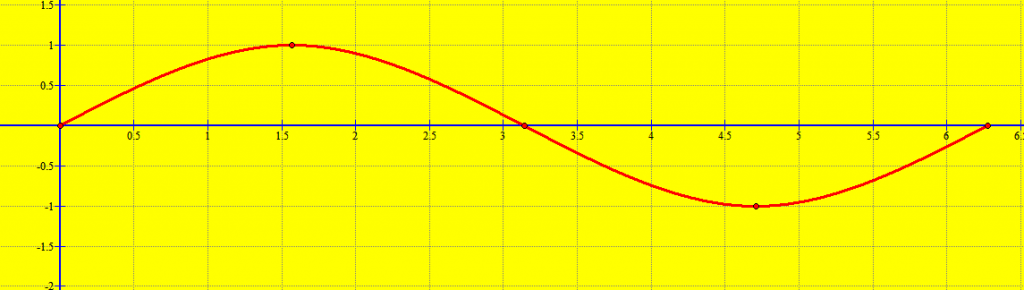
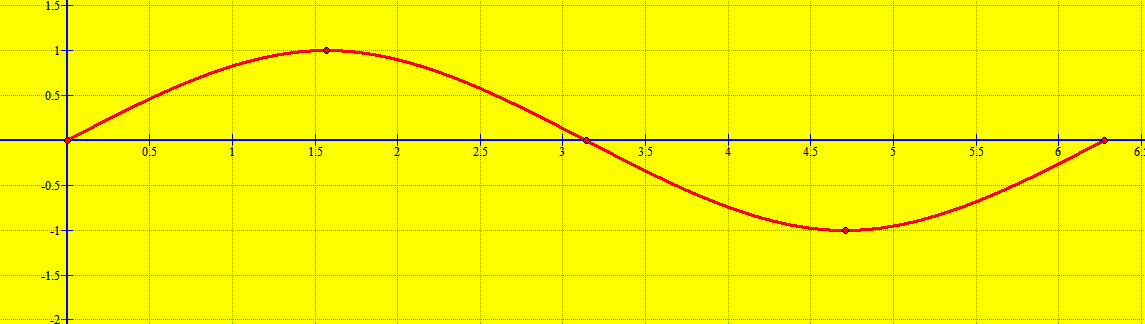
Ndërtojmë tabelën e vlerave të x në segmentin $\displaystyle \left[ 0,2\pi \right]$ :

x	0	$\displaystyle \frac{\pi }{2}$	$\displaystyle \pi$	$\displaystyle \frac{3\pi }{2}$	$\displaystyle 2\pi$
sinx	0	1	0	-1	0

Pikat karakteristike janë:

$\displaystyle A\left( 0;0 \right)$ , $\displaystyle B\left( \frac{\pi }{2};1 \right)$ , $\displaystyle C\left( \pi ;0 \right)$ , $\displaystyle D\left( \frac{3\pi }{2};-1 \right)$ , $\displaystyle E\left( 2\pi ;0 \right)$ .

Nga këto të dhëna ne ndërtojmë grafikun e funksionit $\displaystyle y=\sin x$ .

Kemi parasysh që $\displaystyle \pi \approx 3.14$ .

Funksioni $\displaystyle y=\sin x$ është funksion periodik me period $\displaystyle 2\pi$ .

Grafiku i funksionit $\displaystyle y=\sin x$ , $\displaystyle x\in R$ , që quhet sinusoiudë, merret duke përsëritur pjesën e vet për $\displaystyle x\in \left[ 0,2\pi \right]$ , në sasi të pafundme herësh, majtas e djathtas.

Variacioni i sinusit

Variacioni i kosinusit

Sipas përkufizimit, kosinusi i harkut

*** QuickLaTeX cannot compile formula:
\displaystyle \overset\froën{AM}

*** Error message:
Invalid UTF-8 byte sequence (m@th).
leading text: $\displaystyle \overset\fro

me vlerë x, është i barabartë me abshisën e pikës M.

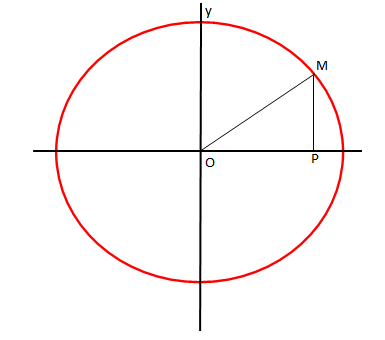
Pra, gjatësia e segmentit $\displaystyle \left[ OP \right]$ tregon vlerën e $\displaystyle \cos x$ .

Për të parë si ndryshon $\displaystyle \cos x$ , mjafton të shohim si ndryshon abshisa e pikës M.

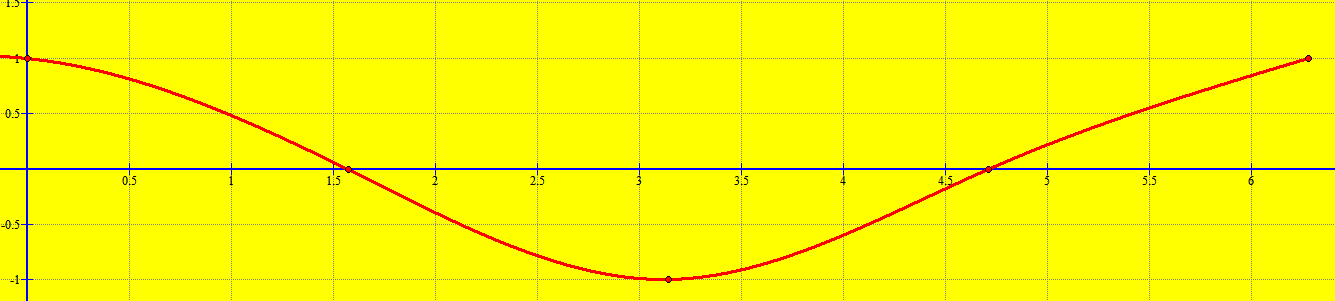
Ndërtojmë tabelën e vlerave të funksionit $\displaystyle y=\cos x$ në segmentin $\displaystyle \left[ 0,2\pi \right]$ .

x	0	$\displaystyle \frac{\pi }{2}$	$\displaystyle \pi$	$\displaystyle \frac{3\pi }{2}$	$\displaystyle 2\pi$
cosx	1	0	-1	0	1

Pikat karakteristike të funksionit $\displaystyle y=\cos x$ janë:

$\displaystyle A\left( 0;1 \right)$ , $\displaystyle B\left( \frac{\pi }{2};0 \right)$ , $\displaystyle C\left( \pi ;-1 \right)$ , $\displaystyle D\left( \frac{3\pi }{2};0 \right)$ , $\displaystyle D\left( 2\pi ;1 \right)$ .

Meqënëse kosinusi është funksion periodik me period $\displaystyle 2\pi$ , grafiku i tij për $\displaystyle x\in R$ merret duke përsëritur një sasi të pafundme herësh, majtas e djathtas , pjesën e tij për $\displaystyle x\in \left[ 0,2\pi \right]$ .

Variacioni i kosinusit