
Rrethi
Përkufizim: “Rrethi është figura gjeometrike e përbërë nga të gjitha pikat e planit, që kanë të njëjtën largesë (të dhënë) nga një pikë fikse (e dhënë)”.
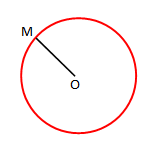
Rrethi
Pika fikse e dhënë quhet qëndër e rrethit.
Segmenti që bashkon qëndrën e rrethit me ndonjë pikë të rrethit quhet rreze e rrethit.
Segmenti OM është rreze e rrethit.
Nga përkufizimi rrjedh që të gjitha rrezet e rrethit kanë të njëjtën gjatësi.
Segmenti që bashkon dy pika të rrethit quhet kordë e tij.
Korda që kalon nëpër qëndër quhet diametër.
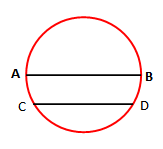
[AB] është diametër i rrethit, ndërsa [CD] është një kordë e rrethit.
Është e qart që qëndra e rrethit është mes i çdo diametric të tij. Gjatëesia e diametrit është sa dyfishi i gjatësisë së rrezes.
Teoremë: “Drejtëza që kalon nga rrezja e rrethit dhe është pingule me një kordë të tij, është përmesore e kësaj korde”.
Sipërfaqja dhe perimetri i rrethit
Sipërfaqja e rrethit me rreze R është .
Perimetri i rrethit me rreze R është .
Shembull 1
Gjeni sipërfaqen dhe perimetrin e rrethit me rreze cm.
Zgjidhje
Duke zbatuar formulën e sipërfaqes së rrethit, kemi:
.
Gjejmë perimetrin e rrethit, duke zbatuar formulën:
.
Përgjigje: Sipërfaja e rrethit me rreze 3 cm është , ndërsa perimetri është
.
Shembull 2
Gjeni diametrin e rrethit me sipërfaqe .
Zgjidhje
Nga formula e sipërfaqes së rrethit, gjejmë fillimisht rrezen e tij:
.
Diametri i rrethit është dy herë më i madh se rrezja e tij. Shkruajmë:
Përgjigje: Diametri i rrethit me sipërfaqe është
Tangjentja ndaj rrethit. Veti të saj
Përkufizim: “Drejtëza e hequr nëpër një pikë të rrethit, pingule me rrezen që kalon nëpër këtë pikë, quhet tangjente”.
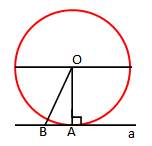
Drejtëza a është tangjetja, ndërsa pika A quhet pikë e tangjentes.
Teoremë 1: “Tangjetja me rrethin nuk ka me të pika të tjera të përbashkëta, veç pikës së tangjentes”.
Teoremë 2: “Segmentet e tangjenteve ndaj rrethit, të hequra nga një pikë jashtë tij janë kongruente dhe formojnë kënde të barabartë me drejtëzen që kalon nëpër këtë pikë dhe qëndrën e rrethit”.
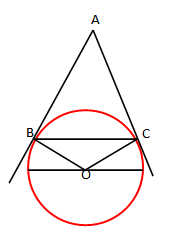
Pra, nga teorema kemi:
Vërtetim. Heqim drejtëzën AO.
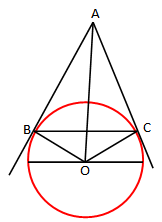
Marrim në shqyrtim trekëndëshat AOB dhe AOC.
Kemi:
- Trekëndëshat AOB dhe AOC janë trekëndësha kënddrejt
- AO brinjë e përbashkët
- OB = OC si rreze të rrethit
Nga teorema 4 e kongruencës së trekëndëshave kënddrejt, e cila thotë: “Nëse hipotenuza dhe njëri katet i një trekëndëshi kënddrejt, janë përkatësisht kongruentë me hipotenuzën dhe njërin katet të një tjetër trekëndëshi kënddrejt, atëherë këta trekëndësha janë kongruentë”, kemi që .
Nga vetitë e kongruencës së trekëndëshave, do te kemi: dhe
.

