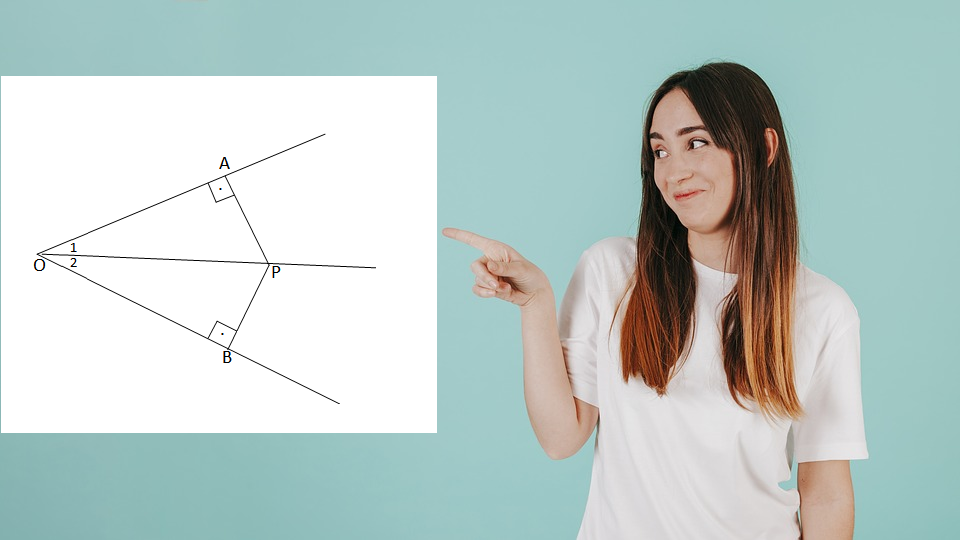
Permesorja
Përkufizim: “Permesorja e segmentit quhet drejtëza pingule me segmentin në mesin e tij”.
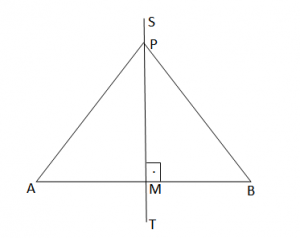
Permesorja e kendit
AM = MB
AP = PB
Vetitë e përmesores së segmentit
Teoremë 1: “Çdo pikë e përmesores së segmentit ka largësi të barabartë nga skajet e segmentit”.
Teoremë 2(e anasjellta e teoremës 1): “Çdo pikë e planit që ka largësi të barabartë nga skajet e segmentit, ndodhet në përmesoren e segmentit”.
Përgjysmorja e kendit
Përkufizim: “Përgjysmorja e një kendi quhet gjysmedrejtëza që ka origjinën në kulmin e kendit dhe e ndan atë në dy pjesë kongruente”.
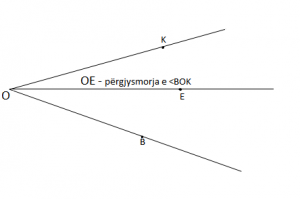
Pergjysmorja e kendit
OE – Përgjysmorja e
Vetitë e përgjysmores
Teorema 1: “Çdo pikë e përgjysmores së kendit e baraslarguar nga brinjët e këndit”.
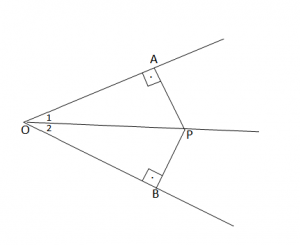
Kushti:
- P është një pikë çfarëdo e përgjysmores OP
Përfundimi:
- PA = PB
Për vërtetimin e kësaj, do të përdorim kriterin e dytë të kongruencës së trekëndëshave.
Marrim në shqyrtim dhe
Dimë që:
nga vetia e përgjysmores.
- Brinja OP e përbashkët
, sepse
dhe
dhe
si diferencë nga 180º.
Teoremë 2 (e anasjellta e teoremës 1): “Çdo pikë që ka largësi të barabartë nga brinjët e këndit, ndodhet në përgjysmoren e këndit”.
Ushtrimi 1
Ndërtoni një kend të ngushtë dhe ndërto përgjysmoren e tij.
Zgjidhje
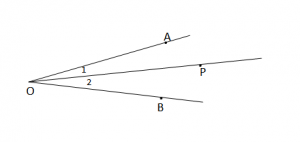
OP – Pergjysmorja e kendit AOB.
Ushtrimi 2
Vizato një kënd të gjerë dhe ndërto përgjysmoren e tij.
Zgjidhje
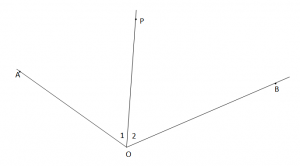
OP – Pergjysmorja e kendit AOB.

