Vecimi i shkronjes ne formula | Gjetja e vleres se nje ndryshori

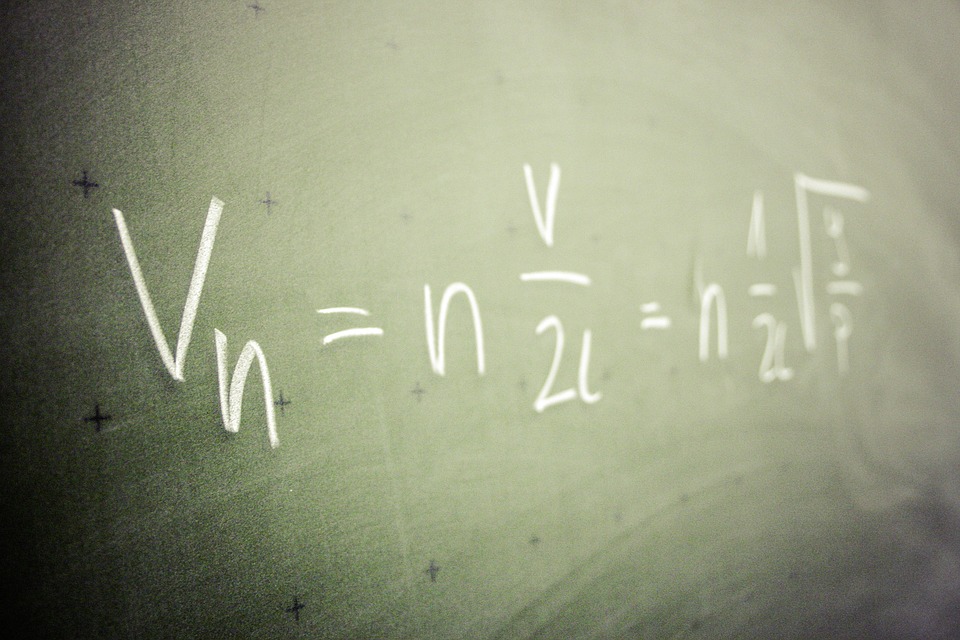
Të veçosh një shkronjë në një formulë, duhet që kjo shkronjë të mbetet e vetme në njërën anë tek formula.

Në çdo shkencë përdoren formulat, por më shumë në matematikë dhe fizikë.

Formula është një ekuacion që përdorë një shprehje për të paraqitur një madhësi të caktuar.

Për shembull, formula e perimetrit të drejtkëndëshit është:

P = 2 (a + b) ose P = 2a + 2b

P – Perimetri i drejtkendëshit

a – Gjatësia e drejtkëndëshit

b – Gjerësia e drejtkëndëshit

Ne duhet të mësojmë të veçojmë çdo madhësi, në varësi të madhësive te tjera, që bëjnë pjesë në këtë formulë:

P = 2a + 2b

Për të veçuar madhësitë që duam, do të përdorim vetitë e veprimeve matematikore.

Shembull 1

Veçoni shkronjën a dhe b tek formula e perimetrit të drejtkëndëshit.

Zgjidhje

Ne fillim veçojmë shkronjën a:

P = 2a + 2b

P – 2b = 2a

$\displaystyle \frac{P-2b}{2}=a$

$\displaystyle a=\frac{P-2b}{2}$

Veçojmë shkronjën b:

P = 2a + 2b
P – 2a = 2b
$\displaystyle \frac{P-2a}{2}=b$

$\displaystyle b=\frac{P-2a}{2}$

Shembull 2

Jepet formula l = v ∙ t

l – rruga

v – shpejtësia

t – koha

Shprehni v në varësi të l dhe t, si dhe t në varësi të l dhe v.

Zgjidhje

Veçojmë v:

l = v ∙ t

$\displaystyle \frac{l}{t}=v$

$\displaystyle v=\frac{l}{t}$

Veçojmë t:

l = v ∙ t

$\displaystyle \frac{l}{v}=t$

$\displaystyle t=\frac{l}{v}$

Shembull 3

Jepet formula $\displaystyle d=\frac{m}{v}$ , ku:

d – dëndësia e lëndës

m – masa e trupit

v – vëllimi i trupit

Veçoni shkronjën v.

Zgjidhje

$\displaystyle d=\frac{m}{v}$

$\displaystyle dv=m$

$\displaystyle v=\frac{m}{d}$

Gjetja e vlerës së një ndryshori në një formulë

Në zgjidhjen e problemave të ndryshme, kur për to ka formula, problema jep vlerat e disa madhësive që bëjnë pjesë në formulë dhe kërkon vlerën e njërës madhësi (ato paraqiten me ndryshore).

Shembull 1

Gjej vlerën e v tek formula $\displaystyle d=\frac{m}{v}$ , kur është dhënë m = 28 kg dhe $\displaystyle d=4kg/{{m}^{3}}$ .

Zgjidhje

Për zgjidhjen e këtij problemi, në fillim veçojmë shkronjën v, sipas vetive të veprimeve matematikore:

$\displaystyle d=\frac{m}{v}$

$\displaystyle dv=m$

$\displaystyle v=\frac{m}{d}$

Tani që veçuam shkronjën v, bëjmë zëvëndësimet:

$\displaystyle v=\frac{28kg}{4kg/{{m}^{3}}}$

$\displaystyle v=7{{m}^{3}}$

Shembull 2

Në formulën e numrave tek B = 2n+1 gjeni vlerën e B-së për n: 0,1,2,3,4.

Zgjidhje

Bëjmë zëvëndësimet.

Për:

n = 0, B = 2 ∙ 0 + 1 = 1
n = 1, B = 2 ∙ 1 + 1 = 3
n = 2, B = 2 ∙ 2 + 1 = 5
n = 3, B = 2 ∙ 3 + 1 = 7
n = 4, B = 2 ∙ 4 + 1 = 9