Teorema e tri pinguleve

Teorema 1: “Drejtëzat e planit, e cila kalon nga këmba e një të pjerrëte, pingul me projeksionin e saj në plan, është pingul me këtë të pjerrët”.

Teorema e anasjelltë: “Drejtëza e planit, e cila kalon nga këmba e një të pjërrëte, pingul me të, është pingule edhe me projeksionin e saj”.

Shembull 1

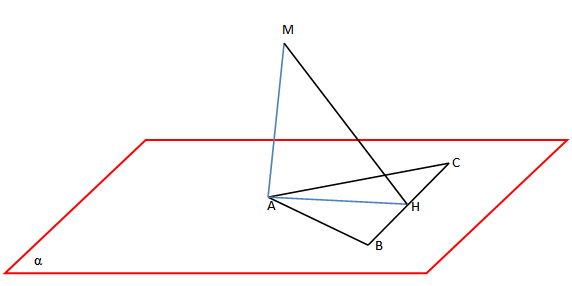
Në trekëndëshin ABC, lartësia AH mbi brinjën BC është 12 cm. Nga kulmi A i tij ndërtohet pingulja me planin e trekëndëshit dhe në të merret pika M, e tillë që AM = 35 cm. të gjendet largesa e pikës M nga brinja BC e trekëndëshit.

Zgjidhje

Bashkojmë pikat M dhe H. meqë MA është pingule me planin e trekëndëshit ABC, del se MH është e pjerrët me këtë plan.

Drejtëza BC është pingule me projeksionin AH të së pjerrëtës MH (teorema e tri pinguleve).

Kjo tregon se largesa e pikës M nga brinja BC e trekëndëshit është segmenti MH.

Në trekendëshin kënddrejtë AMH kemi:

.

cm.

Përgjigje: Largesa e pikës M nga brinja BC e trekëndëshit është 37 cm.

Do të pranojmë pa vërtetim këto teorema:

Teorema 1: “Në qoftë se dy drejtëza janë pingule më një plan, atëherë ato janë paralele ndërmjet tyre”.

Teorema 2: “Në qoftë se një plan është pingul me njërën prej dy drejtëzave paralele, atëherë ai është pingul edhe me tjetrën”.

Drejteza paralele me planin

Përkufizim: “Drejtëza d dhe plani α quhen paralelë, në qoftë se nuk kanë asnjë pikë të përbashkët”.

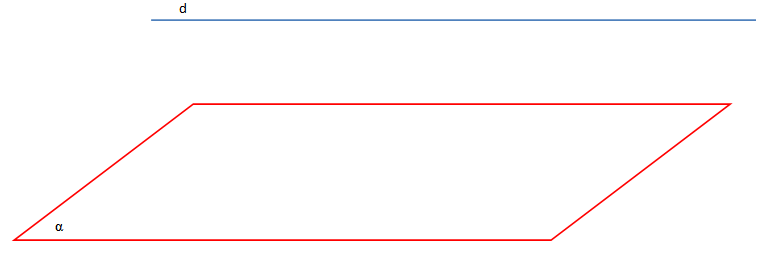
Në këtë figurë, drejtëza d është paralele me planin α. Shkruajmë .

Kemi teoremat:

Teorema 1: “Çdo drejtëz paralele me një drejtëz të një plani është paralele me këtë plan”.

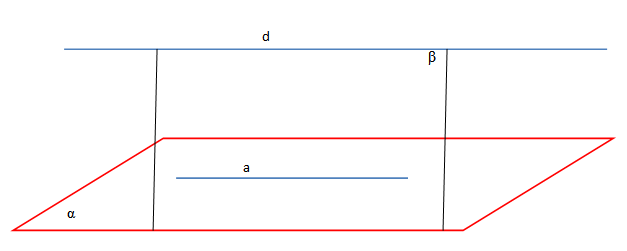
Teorema 2: “Në qoftë se ng një drejtëz d, paralele me një plan α, ndërtojmë një plan β, i cili pret planin α, atëherë drejtëza e ndërprerjes është paralele me drejtëzën d”.