Mbledhja e numrave natyrorë. Ushtrime dhe problema me mbledhje.

 

Mbledhja përkufizohet si numërim i shkurtuar, d.m.th. mbledhësit të parë i shtohen njëshet, një nga një, të mbledhësit të dytë (për shembull numri 16 ka 16 njëshe ).

Ju tashmë jeni  njohur me vetitë e mbledhjes dhe të zbritjes  që më herët. Tani duhet të përsëriten ato veti dhe duhet treguar se vlejnë për të gjithë bashkësinë e numrave natyrorë N. Plotësimi i dhjetëshëve , qindëshëve do të na ndihmojë më shumë për të kryer shpejt veprime me mend.

Në mënyrë grafike janë paraqitur disa barazime, saktësia e të cilave është e qartë:

(1) a + b = S

(2) S – a = b

(3) S – b = a

 

P.sh numrin 10 e gjejmë si shumë e dy numrave natyrorë:

10 = 5 + 5

10 = 1+ 9

10 = 7 +3

10 = 6 + 4

10 = 8 + 2

Pra, shohim që numri 10 shprehet si shumë e dy numrave natyrorë 5 herë.

Le të marrim shumën e dy numrave natyrorë:

• 18 + 12 = 30 ( sepse mbledhim si fillim njëshet e numrave 2 + 8 = 10, nga ana tjetër na mbeten 10 + 10 = 20 . Atëherë do të kemi 20 + 10 = 30) .
• 49 + 11 = 60 ( mbledhim si fillim njëshet 9 + 1 = 10, dhe na mbeten 40 + 10 = 50. Atëherë do të kemi 50 + 10 = 60)
• 16 + 21 + 4 + 39 = (16  + 4) + ( 21 + 39 ) = 20 + 60 = 80
• 2 + 1 8 + 24 + 46 = (2+18 ) + (24 +46 ) = 20 + 70 = 90
• 100 – 38 = 62 ( 10 – 8 = 2 dhe 9 – 3 = 6 pra 0 i njëshes bëhet 10 sepse i‘a merr një vlerë dhjetëshes dhe vlera e dhjetëshes bëhet 9)
• 93 – 12 = 81 ( sepse zbresim njëshet si fillim 3 – 2 = 1 dhe më pas dhjetëshet  9 – 1 = 8 )

 

Ushtrimi 1

Cilat nga numrat dhjetorë jep rezultatin 1?

Zgjidhje:

Për të mbledhur dy numra dhjetorë dhe shuma e tyre të jetë 1, si fillim duhet të shikojmë se si të mbledhim numrat pas presjes dhe që shuma e tyrë të japi 10. Atëherë le ta konkretizojmë në ushtrimin përkatës:

0.3 + 0. 7 = 1 ( sepse shuma e numrave 3 + 7 = 10 )

0.4 + 0.6 = 1 ( sepse 6 + 4 = 10)

0.9 + 0.1 = 1  (sepse 9 + 1 = 10 )

0.5 + 0.5 = 1  ( sepse 5 + 5 = 10 )

0.2 + 0.8 = 1  (sepse 2 + 8 = 10 )

 

 

Ushtrimi 2

Gjej numrat që mungojnë

 

Zgjidhje:

 

 

 

 

 

Problema me mbledhje

U njohëm me mbledhjen e dy numrave natyrorë , tashmë do të njihemi me problemat. Pra hapi i parë të kthejmë problemin nga jeta e përditshme në një problem matematikor për të gjetur shifrat e sakta të zgjidhjes. Si të mbledhim numra me qindëshe. P.sh:

235 + 358

= (200 +30 +5 )  + ( 300 + 50 + 8 )

= (200 + 300 ) + ( 30 + 50 ) + ( 5+ 8 )

= 500 + 80 + 13

= 593 ( e rrumbullakosim si 600 )

Problema 1

Në një biliotekë ndodhen 8655 libra matematike. Në një tjetër bibliotekë janë 7 525 libra  dhe në një tretë  janë  8112 libra . Gjej se sa ka në të trija bibliotekat së bashku.

 

Zgjidhje:

Biblioteka e parë ka 8655

Biblioteka e dytë ka 7525

Biblioteka e tretë ka 8112

Për të gjetur se sa libra ndodhen në bibliotekë, ne i mbledhim të trija shumat e librave që janë në secilën biliotekë:

8655 + 7525 + 8112 (secili nxënës mund t`i mbledhi në mënyrën më të mirë të mundshme që ai e sheh si më të thjeshtë)

Atëherë i mbledhim me njërën nga mënyrat, në rastin tonë i mbledhim me mënyrën 5 dhe do të kemi:

86 55 + 7525 + 8112

= ( 8000 + 600 + 50 + 5 ) +  ( 7000 + 500 + 20 + 5 ) + ( 8000 + 100 + 10 + 2 ), i shkruajtëm numrat në formë të zbërthyer.

Hapi që ndjekim në vijim:  Mbledhim mijëshet veç, qindëshet veç, dhjetëshet veç dhe njëshet veç. Kemi :

= ( 8000 + 7000 + 8000 ) + ( 600 + 500 + 100 ) + (50 + 20 + 10 ) + ( 5 + 5 + 2)

= 23 000 + 1200 + 80 + 12

=24 292.

Përgjigje: Pra, në bibliotekë ndodhen 24 292 libra  (Njëzet e katërmijë e dyqind e nëntëdhjetë e dy libra), duke e rrumbullakosur në mijëshen  më të afërt  24 29224 000 libra )

 

 

Problema 2

Një postier shpërndan 418 letra në lagjen e parë, 1607 në lagjen e dytë  dhe 988 letra në lagjen e tretë. Sa letra shpërndau në të trija lagjet së bashku?

 

Zgjidhje

Në të njëjtën mënyrë sikurse vepruam tek problema më lart, veprojmë edhe tek ushtrimi ynë përkatës. Atëherë kemi:

Lagje nr 1 shpërndau  418 letra.

Lagje nr 2 shpërndau  1607 letra.

Lagje nr 3 shpërndau 988 letra.

 

I mbledhim te treja numrat dhe kemi

418 + 1607 + 988 =

= (400 + 10 + 8 ) + (1000 + 600 + 0 + 7 ) + ( 900 + 80 + 8)

= 1000 + ( 400 + 600 + 900 ) + ( 10 + 0 + 80 ) + ( 8 + 7 + 8 )

= 1000 +  1900 + 90 + 23

= 3013 letra

Përgjigje: Postieri ka shpërndarë gjithësej 3013 letra nëpër lagje.

 

Problema 3

Beni kishte 345 lekë. Ai bleu 210  lekë biskota, 120 lekë çokollata. Sa lekë i mbetën Benit?

Zgjidhje:

Gjithësej beni kishte 345 lekë.

Ai bleu 210 lekë biskota + 120 lekë cokollata =  330 lekë të shpenzuara në total.

Atëherë kemi: 345 – 330 = 15 lekë.

Përgjigje: Benit i mbetën kusur 15 lekë .

 

 

 

 

Zbritja e numrave natyrorë.  Ushtrime dhe problema me zbritje

Zbritja është  veprimi i kundërt i mbledhjes. Zbritjen e quajme ndryshe edhe ndryshesë.

Më poshtë kemi ndryshesën e dy numrave:

Ushtrime:

1. 672 – 320. Mënyra që këmi zgjedhur për këtë veprim është si më poshtë:

I shprehim numrat 653 dhe 231  si zbërthim faktorësh.

(600 + 50 + 3) – ( 200 +30 +1 )  => zbresim qindëshet veç , dhjetëshet veç dhe njëshet veç.

= (600 – 200 ) + (50 – 30 ) +( 3- 1 )

= 400 + 20+ 2

= 422

ose veprojmë edhe në një mënyrë tjetër më të thjeshtë si më poshtë:

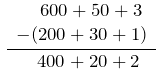
Pra  653 – 231 = 422

 

2. 884 – 213 = 671

Veprojmë në të njëjtën mënyrë si tek shembulli më lart:

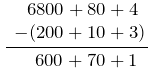
Pra, zbresim qindëshet me qindëshet, dhjetëshet me dhjetëshet, njëshet me njëshet ose më qartë veprojmë:

800 – 200 = 600

80 – 10 = 70

4 – 3 = 1 dhe shuma e numrave 600+70+1 = 671, pra, numri është  671 është diferëenca e numrave 884 – 213.

 

Problema me zbritje

Ne mund te veprojmë edhe në një menyrë tjetër për të kryer diferencën. Ne mund te bëjmë provën e zbritjes me anë të mbledhjes.

P.sh:

420 – 200 = 220

E shkruajmë në formën e mbledhjes:

220 + 200 = 420

 

Ushtrimi 1

• Kryeni zbritjen dhe bëni provën.

1. 653 – 278 = 375        |  prova:  375 + 278 = 653
2. 1415 – 365 = 1050    |  prova:  1050 + 365 = 1415
3. 1352 – 1345 = 7        |  prova:  1352 + 7 = 1352

 

Problema 1

• Arjoni shiti 689 pjesë në qershor dhe 908 në korrik

a) Sa pjesë shiti gjithësej?

b) Sa pjesë më shumë shiti në korrik sesa në qershor?

 

Zgjidhje:

Në muajin qershor ai shiti 689 + 908 që shiti në muajin korrik është e barabartë me 1597.

a) Matematikisht kemi 689 + 908 = 1579 . Gjithësej arjoni shiti 1579 pjesë.

b) 908- 689 = 219 pjesë shiti më shumë në korrik se sa në muajin qershor.

 

 

Problema  2:

Shtëpia e Arjanës është 910 m larg nga shkolla, shtëpia e Erdit është 345 m larg nga shkolla. Sa metra larg është shtëpia e Arjanës nga ajo e Erdit?

 

Zgjidhje:

Duke qënë se shtëpia e Arjanës  është 910 m larg nga shkolla dhe shtëpia e Erdit është 345, për të gjetur largesën ndërmjet shtëpisë së Arjanës dhe shtëpisë së Erdit gjejmë diferencën e numrave përkatës ndërmjet shtëpive. Kemi:

910 – 345 = 565 m është larg shtëpia e Arjanës nga ajo e Erdit .

 

Problema 3

Në secilën nga kutitë gjenden nga 5000 pjesë  që kanë të bëjnë me përdorimin e kompjuterit . në fund të ditës, Arditi numëroi sa copë kishin mbetur  pa shitur dhe i shënoi në kuti si në figurë .

Sa pjesë kishte për të shitur gjithësej kur filloi punën?

Zgjidhje:

Duke qënë se në cdo kuti gjenden nga 5000 pjesë, ne kemi 4 kuti për nga 5000 pjesë secila. Rezultonë që shuma e katër kutive është  :

5000 + 5000 + 5000+ 5000 = 20 000 pjesë.

Përgjigje: Pra,  Arditi kishte për të shitur gjithësej kur filloj punën 20 000 pjesë.