Mbledhja dhe zbritja e vektoreve | Matematika 9

Mbledhja e vektoreve

Përkufizim: “Shumë të vektorit $\displaystyle \vec{a}$ me vektorin $\displaystyle \vec{b}$ quajmë vektorin që ka si fillesë fillesën e vektorit të pare ( $\displaystyle \vec{a}$ ) dhe si mbaresë mbaresën e vektorit të dytë ( $\displaystyle \vec{b}$ ), pasi e kemi zhvendosur $\displaystyle \vec{b}$ me fillesë tek mbaresa e $\displaystyle \vec{a}$ ”.

Shuma e vektorit $\displaystyle \vec{a}$ me vektorin $\displaystyle \vec{b}$ shënohet $\displaystyle \vec{a}+\vec{b}$ .

Rregulli i paralelogramit

Kur vektorët $\displaystyle \vec{a}$ , $\displaystyle \vec{b}$ nuk kanë të njëjtin drejtim, për gjendjen e shumës së tyre mund të përdoret një mënyrë tjetër, që quhet “rregulli i paralelogramit”.

I zhvendosim vektorët jobashkëvizorë $\displaystyle \vec{a}$ , $\displaystyle \vec{b}$ me fillesë në të njëjtën pikë O.

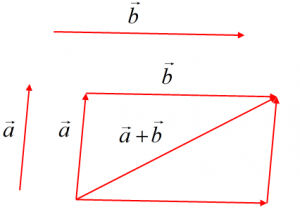
Vektori diagonales së paralelogramit $\displaystyle \vec{a}+\vec{b}$ është shuma e vektoreve $\displaystyle \vec{a}$ , $\displaystyle \vec{b}$ .

Vetitë e mbledhjes së vektoreve

Mbledhja e vektoreve gëzon veti të ngjashme me ato të mbledhjes së numrave.

Vetia e ndërrimit. Për çdo dy vektorë $\displaystyle \vec{a}$ , $\displaystyle \vec{b}$ ka vend barazimi

$\displaystyle \vec{a}+\vec{b}=\vec{b}+\vec{a}$

Vetia e shoqërimit. Për çdo tre vektorë $\displaystyle \vec{a}$ , $\displaystyle \vec{b}$ , $\displaystyle \vec{c}$ ka vend barazimi:

$\displaystyle \left( \vec{a}+\vec{b} \right)+\vec{c}=\vec{a}+\left( \vec{b}+\vec{c} \right)$

Shuma e disa vektoreve

Përkufizim: “Shumë të tre vektoreve $\displaystyle {\vec{a}}$ , $\displaystyle {\vec{b}}$ , $\displaystyle {\vec{c}}$ quajmë shumën e shumës së dy vektorëve të parë me vektorin e tretë. Kjo shumë shënohet $\displaystyle \vec{a}+\vec{b}+\vec{c}$ . Sipas përkufizimit kemi $\displaystyle \vec{a}+\vec{b}+\vec{c}=\left( \vec{a}+\vec{b} \right)+\vec{c}$ ”.

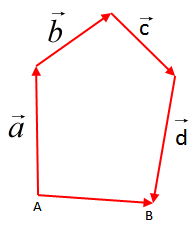
Kemi $\displaystyle AB=\vec{a}+\vec{b}+\vec{c}+\vec{d}$ .

Diferenca e vektoreve

Përkufizim: “Diferencë të vektorit $\displaystyle \vec{a}$ me vektorin $\displaystyle \vec{b}$ quajmë shumën e vektorit $\displaystyle \vec{a}$ me të kundërtin e vektorin $\displaystyle \vec{b}$ ”.

Diferencën e $\displaystyle \vec{a}$ me $\displaystyle \vec{b}$ e shënojmë $\displaystyle \vec{a}-\vec{b}$ . Sipas përkufizimit kemi $\displaystyle \vec{a}-\vec{b}=\vec{a}+\left( -\vec{b} \right)$ .