Kongruenca e trekendeshave | Rastet e kongruences se trekendeshave

Sot do të shohim tri rastet e kongruencës së trekendeshave.

Në figurën më poshtë janë paraqitur dy trekëndësha kongruentë $\displaystyle ABC$ dhe $\displaystyle {{A}_{1}}{{B}_{1}}{{C}_{1}}$

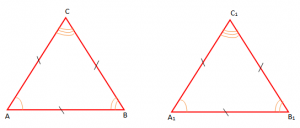
Ata mund ti mbivendosim mbi njëri-tjetrin dhe ata do të puthiten plotësisht.

Vëmë në dukje se: “në trekëndëshat kongruentë, përballë brinjëve kongruente ndodhen këndet kongruente dhe përballë këndeve kongruente ndodhen brinjët kongruente”.

Në figurën më sipër kemi:

Përballë brinjëve kongruente [AB] dhe [A₁B₁] qëndrojnë këndet kongruente $\displaystyle \angle C=\angle {{C}_{1}}$ .

Kur trekëndëshat janë kongruentë, përdoret shënimi: $\displaystyle \vartriangle ABC\equiv \vartriangle {{A}_{1}}{{B}_{1}}{{C}_{1}}$

Rasti I i kongruences së trekendeshave

Teoremë: “Nëse dy brinjë dhe këndi midis tyre i një trekëndëshi, janë përkatësisht kongruentë me dy brinjë dhe këndin midis tyre të një trekëndëshi tjetër, atëherë trekëndëshat janë kongruentë”.

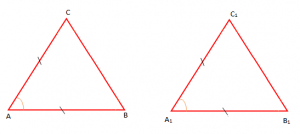
Ky njihet si rasti “Brinje Kënd Brinjë (BKB)”.

Ushtrimi 1

Në figurën më poshtë kemi AB = CD. Vërtetoni që $\displaystyle \vartriangle ABC\equiv \vartriangle ACD$

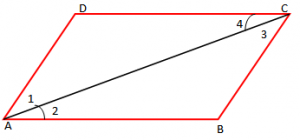
Zgjidhje

Marrim në shqyrtim trekëndëshat ABC dhe ACD.

Kemi:

AB = CD (B)
$\displaystyle \hat{2}=\hat{4}$ si kënde ndërrues të brendshëm (K)
AC brinjë e përbashkët (B)

Në bazë të teoremës së rastit të parë të kongruencës së trekendeshave (BKB), vërtetojmë që $\displaystyle \vartriangle ABC\equiv \vartriangle ACD$ .

Rasti II i kongruences së trekendeshave

Teoremë: “Nëse një brinjë dhe dy këndet anëshkruar më të të një trekëndëshi, janë përkatësisht kongruentë me një brinjë dhe dy kënde të një trekëndëshi tjetër, atëherë këta trekëndësha janë kongruentë”.

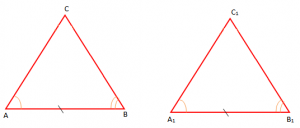
Ky njihet si rasti “Kënd Brinjë Kënd (KBK)”.

Ushtrimi 1

Në figurën më poshtë kemi të dhënë: $\displaystyle AD//BC$ dhe pika O është mësi i brinjës AB. Vërtetoni që $\displaystyle \vartriangle AOD\equiv \vartriangle BOC$

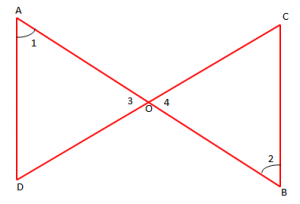
Zgjidhje

Marrim në shqyrtim trekëndëshat AOD dhe BOC.

Kemi:

$\displaystyle \hat{1}=\hat{2}$ , si këndë ndërrues të brendshëm (K)
$\displaystyle AO=OB$ meqë O mes i segmëntit AB (B)
$\displaystyle \hat{3}=\hat{4}$ si kënde të kundërt në kulm (K)

Në bazë të teoremës së rastit të dytë të kongruencës së trekendeshave (KBK), vërtetojmë që $\displaystyle \vartriangle AOD\equiv \vartriangle BOC$ .

Rasti III i kongruences së trekendeshave

Teoremë: “Nëse tri brinjët e një trekëndëshi janë përkatësisht kongruente me tri brinjët e një trekëndëshi tjetër, atëherë keta trekëndësha janë kongruentë”.

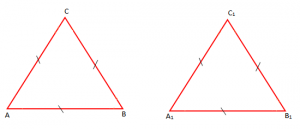
Ky njihet si rasti “Brinjë Brinjë Brinjë (BBB)”.

Ushtrimi 1

Nëpër pikën O të segmëntit [AB], është hequr permesorja e tij. Marrim një pike K në përmesoren e hequr dhe formojmë 2 trekëndësha. Vërtetoni që këta trekëndësha janë kongruentë.

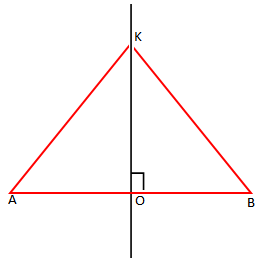
Zgjidhje

Marrim në shqyrtim trekëndëshat AOK dhe BOK.

Kemi:

$\displaystyle AO=OB$ sepse përmesorja e ndanë segmentin [AB] në dy segmente kongruente (B).

$\displaystyle OK$ brinjë e përbashkët e trekendeshave (B).

$\displaystyle AK=BK$ nga vetia e permesores (B).

Në bazë të teoremës së rastit të tretë të kongruencës së trekendeshave (BBB), vërtetojmë që $\displaystyle \vartriangle AOK\equiv \vartriangle BOK$ .