Rrethi jashteshkruar dhe brendashkruar trekendeshit

Rrethi i jashteshkruar trekëndëshit

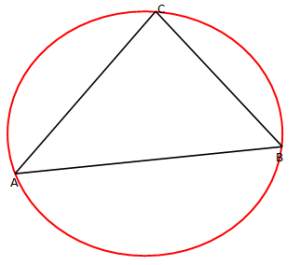
Teoremë: “Çdo trekëndëshi mund ti jashtëshkruhet një rreth”.

Ky është një rreth i jashteshkruar trekëndëshit ABC.

Rrethi që kalon nëpër dy pika

Teoremë: “Çdo rreth që kalon nëpër pikat A dhe B e ka qendrën në përmesoren e segmentit [AB]”.

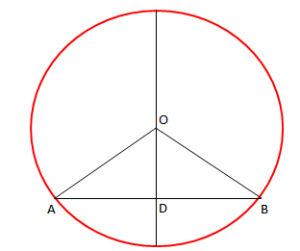
Pika O është qendër e rrethit.

OD përmesore e segmentit [AB].

Vetia e përmesores së trekëndëshit

Teoremë: “Çdo pikë e përgjysmores së një këndi jo të shtrirë ka largesa të barabarta nga brinjët e këndit”.

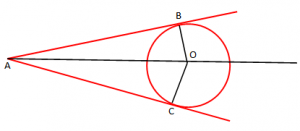
Pra, [OB]=[OA]

Teorema e anasjelltë: “Çdo pikë Brenda këndit, që ka largesa të barabarta nga brinjët e tij, ndodhet në përgjysmoren e këndit”.

Rrjedhim: “Nëse brinjët e një këndi janë tangjente ndaj një rrethi, atëherë qendra e këtij rrethi ndodhet në përgjysmoren e këndit”.

Rrethi i brendashkruar trekëndëshit

Teoremë: “Në çdo trekëndësh mund të brendashkruajmë një rreth”.

Në një trekëndësh të dhënë, mund të përshkruajmë vetëm një rreth.

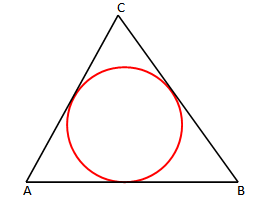
Ky është një rreth i brendashkruar trekëndëshit ABC.

Në trekëndëshin barabrinjës:

Rrezja e rrethit të jashtëshkruar është sa dyfishi i rrezes së rrethit brendashkruar
Rrezja e rrethit të brendashkruar është sa $\displaystyle \frac{1}{3}$ e lartësisë.

Zbatime të trekëndëshave brendashkruar dhe jashteshkruar

Rrethi i jashteshkruar trekëndëshit kënddrejtë

Teoremë: “Rrethi i jashteshkruar trekëndëshit kënddrejtë e ka qendrën në mesin e hipotenuzës”.

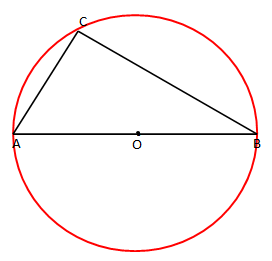
Pra:

$\displaystyle \vartriangle ABC$ është trekëndësh kënddrejtë.

AB është hipotenuza

OA është rrezja e rrethit dhe pika O mesi i hipotenuzës AB

Një formulë tjetër për sipërfaqen e trekëndëshit

Teoremë: “Sipërfaqja e trekëndëshit është e barabartë me gjysmën e prodhimit të perimetrit të tij me rrezen e rrethit brendashkruar”.

Shembull 1

Katetet e një trekëndëshi kënddrejt janë $\displaystyle a=6~cm$ dhe $\displaystyle b=8~cm$ . Gjeni rrezen e rrethit të jashtëshkruar dhe rrezen e rrethit brendashkruar trekëndëshit.