Ekuacioni i fuqise se pare me nje ndryshore | Matematika 10

Ekuacioni i fuqise se pare me një ndryshore

Përkufizim: “Një ekuacion quhet i fuqise se pare me një të panjohur nëse trajta kanonike e tij është ax+b=0”.

Për të zgjidhur ekuacionin e fuqise se pare ax+b=0 do të kryejmë shndërrime të njëvlershme.

Zgjidhje algjebrike.

$\displaystyle ax+b=0$

Kalojmë b-në nga e djathta me shenjë të ndryshuar:

$\displaystyle ax=-b$

Pjesëtojmë të dy anët e ekuacionit me a, $\displaystyle a\ne 0$ .

$\displaystyle \frac{ax}{a}=\frac{-b}{a}$

Thjeshtojmë në anën e majtë:

$\displaystyle x=\frac{-b}{a}$ .

Zgjidhja e ekuacionit $\displaystyle ax+b=0$ është bashkësia $\displaystyle A=\left\{ -\frac{b}{a} \right\}$ .

Shembull 1

Të zgjidhen ekuacionet:

a) $\displaystyle 3x+6=0$

b) $\displaystyle 2x+7=x-4$

c) $\displaystyle \frac{3x+1}{3}=\frac{x}{2}+3$

Zgjidhje

a) $\displaystyle 3x+6=0$

Kalojmë 6 në anën tjetër duke i ndryshuar shenjën:

$\displaystyle 3x=-6$

Pjesëtojmë me 3 të dy anët dhe thjeshtojmë anën e majtë:

$\displaystyle \frac{3x}{3}=\frac{-6}{3}$

$\displaystyle x=\frac{-6}{3}=-2$ .

Përgjigje: Zgjidhje e ekuacionit $\displaystyle 3x+6=0$ është bashkësia $\displaystyle A=\left\{ -2 \right\}$ .

b) $\displaystyle 2x+7=x-4$

Kalojmë ndryshoret në një anë dhe numrat në anën tjetër dhe kryejmë veprimet:

$\displaystyle 2x-x=-4-7$

$\displaystyle x=-11$

Përgjigje: Zgjidhje e ekuacionit $\displaystyle 2x+7=x-4$ është bashkësia $\displaystyle A=\left\{ -11 \right\}$ .

c) $\displaystyle \frac{3x+1}{3}=\frac{x}{2}+3$

Shumëzojmë me 6 gjithë kufizat e ekuacionit për të zhdukur thyesat:

$\displaystyle 6\cdot \frac{3x+1}{3}=6\cdot \frac{x}{2}+6\cdot 3$

$\displaystyle 6x+2=3x+18$

Kalojmë ndryshoret në një anë dhe numrat në anën tjetër dhe kryejmë veprimet:

$\displaystyle 6x-3x=18-2$

$\displaystyle 3x=16$

Pjesëtojmë me 3 të dy anët dhe thjeshtojmë anën e majtë:

$\displaystyle \frac{3x}{3}=\frac{16}{3}$

$\displaystyle x=\frac{16}{3}$

Përgjigje: Zgjidhje e ekuacionit $\displaystyle \frac{3x+1}{3}=\frac{x}{2}+3$ është bashkësia $\displaystyle A=\left\{ \frac{16}{3} \right\}$

Numri i zgjidhjeve të ekuacionit të fuqisë së parë me një ndryshore

Tani do të mesojmë se çfarë kushtesh duhet të plotësojë një ekuacion i fuqisë së parë me një ndryshore, kur ai merr trajtën ax = b.

Ekuacioni ka një rrënjë kur:

$\displaystyle a\ne 0$

$\displaystyle a\ne 0$ ose $\displaystyle b=0$

Forma që merr ekuacioni në këto raste është:

$\displaystyle x=\frac{b}{a}$ , kur $\displaystyle a\ne 0$ dhe $\displaystyle a\ne 0$

$\displaystyle ax=0$ , kur b = 0

$\displaystyle x=\frac{0}{a}=0$

Ekuacioni ka një pafundësi rrënjësh kur:

a = 0 dhe b = 0

Në këtë rast do të kishim:

$\displaystyle x=\frac{0}{0}$ , ndaj ekuacioni ka një pafundësi zgjidhjesh.

Ekuacioni s’ka rrënjë kur:

a = 0, $\displaystyle b\ne 0$

Në këtë rast do të kishim:

0 ∙ x = b

0 = b (ne kemi kushtin që $\displaystyle b\ne 0$ ), ndaj ekuacioni s’ka zgjidhje.

Zgjidhja grafike e ekuacionit të fuqise se pare

Ekuacioni i fuqise se pare me një ndryshore është një funksion linear.

Të zgjidhësh grafikisht ekuacionin ax+b=0 do të thotë të gjesh pikat ku drejtëza y=ax+b pret boshtin X’X.

Shembull 1

Të zgjidhet grafikisht ekuacioni $\displaystyle 2x+4=0$

Zgjidhje

Ndërtojmë drejtëzën me ekuacion y=2x+4.

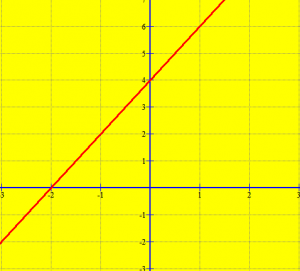
Pika ku drejtëza me ekuacion y=2x+4 ka prerë boshtin X’X e ka abshisën x=-2. Pra, rrenja e ekuacionit 2x+4=0 është x=-2.

Shembull 1

Zgjidhje

Numri i zgjidhjeve të ekuacionit të fuqisë së parë me një ndryshore

Ekuacioni ka një rrënjë kur:

Ekuacioni ka një pafundësi rrënjësh kur:

Ekuacioni s’ka rrënjë kur:

Zgjidhja grafike e ekuacionit të fuqise se pare

Shembull 1

Zgjidhje

Postime te ngjashme: