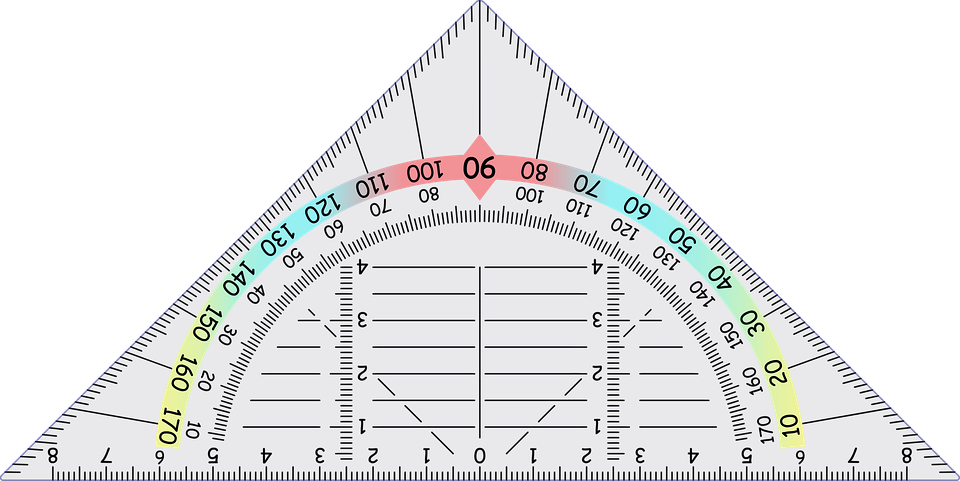
Kende dhe drejteza

kende dhe drejteza

Matja e kendeve. Masa e tyre

Përkufizim: “Të matësh një kend, do të thotë të gjesh numrin e njësive ose nënfishave të njësisë që përmbanë kendi”.

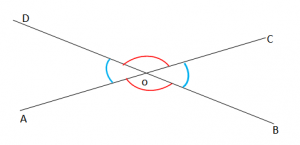
Kendet e kundert ne kulm

Në fillim mësojmë çfarë janë vërtetimet dhe teoremat, pastaj shikojmë teoremat për kendet e kundërt në kulm.

Përkufizim 1: “Arsyetimet për të provuar vërtetësinë e një fjalie matematike, quhen vërtetime”.

Përkufizim 2: “Fjalitë matematike, për vërtetësinë e të cilave bindemi me anë të vërtetimit, quhen teorema”.

Çdo teoremë ka 2 pjesë:

Kushti: do të thotë çfarë është e dhënë si e vërtetë
Përfundimi: do të thotë çfarë kërkohet të vërtetojmë.

Teorema 1: “Nëse dy kende janë të kundërt në kulm, atëherë ata janë kongruentë”.

Pra: $\displaystyle \angle AOB=\angle DOC$

$\displaystyle \angle AOD\text{ }=\angle BOC$

Kendet shtues dhe plotësues

Ashtu siç kemi mësuar në klasën e gjashtë:

Dy kende quhen shtues, kur shuma e tyre është 180º.

Dy kende quhen plotësues, kur shuma e tyre është 90º.

Shembull 1

Jepet këndi 35º. Gjeni plotësuesin e tij.

Zgjidhje

Nga përkufizimi dimë që shuma e dy këndeve plotësues është 90º, pra do të kemi:

x + 35 = 90

x = 90 – 35

x = 55º.

Shembull 2

Jepet kendi 120º. Gjeni shtuesin e tij.

Zgjidhje

Nga përkufizimi dimë që shuma e dy këndeve shtues është 180º, pra do të kemi:

x + 120 = 180

x = 180 – 120

x = 60º.

Drejtëzat paralele

Përkufizim: “Nëpër një pikë jashtë një drejtëze mund të ndërtohet vetëm një drejtëz paralele me drejtëzën e dhënë”.

Shohim shembullin:

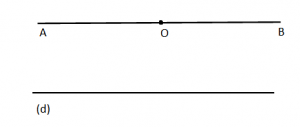
Pra, jashtë drejtëzës (d) ne kemi ndërtuar një pikë O, nga e cila kemi hequr drejtëzën AB, paralele me drejtëzën (d).

Kendet që formohen nga dy drejtëza paralele dhe një prerëse e tyre

Kemi të dhënë $\displaystyle {{d}_{1}}||{{d}_{2}}$ .

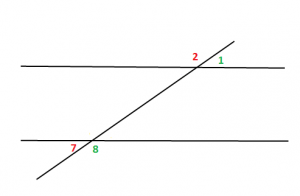
Formohen 8 kende, si në figurën më poshtë:

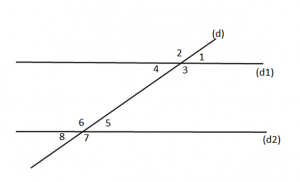
Kemi disa lloje kendesh:

Kende ndërrues të brendshëm

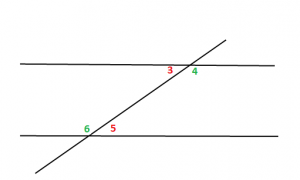
Tek kendet ndërrues të brendshëm, kendet janë dy nga dy të barabartë.

Pra, do të kemi:

$\displaystyle \angle 3\equiv \angle 5$
$\displaystyle \angle 4\equiv \angle 6$

2) Kende ndërrues të jashtëm

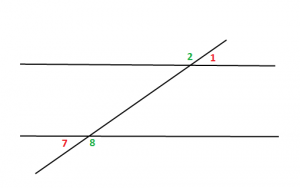
Tek kendet ndërrues të brendshëm, kendet janë dy nga dy të barabartë.

Pra, do të kemi:

$\displaystyle \angle 1\equiv \angle 7$
$\displaystyle \angle 2\equiv \angle 8$

3) Kende përgjegjës

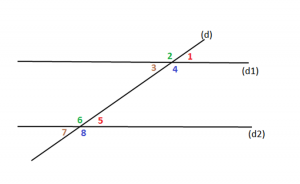
Pra, do të kemi:

$\displaystyle \angle 1\equiv \angle 5$
$\displaystyle \angle 2\equiv \angle 6$
$\displaystyle \angle 3\equiv \angle 7$
$\displaystyle \angle 4\equiv \angle 8$

4) Kende të njëanshëm të brendshëm

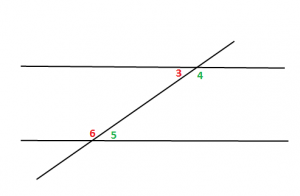
Tek kendet të njëanshëm të brendshëm, kendet janë dy nga dy shtues.

Pra, do të kemi:

$\displaystyle \angle 3+\angle 6={{180}^{{}^\circ }}$
$\displaystyle \angle 4+\angle 5={{180}^{{}^\circ }}$

5) Kende të njëanshëm të jashtëm

Tek kendet të njëanshëm të jashtëm, kendet janë dy nga dy shtues.

Pra, do të kemi:

$\displaystyle \angle 2+\angle 7={{180}^{{}^\circ }}$
$\displaystyle \angle 1+\angle 8={{180}^{{}^\circ }}$

Më poshtë janë të vërteta pohimet e anasjellta të pohimeve të treguara më lart në pikat 1-5.

”Nëse dy kendet ndërrues të brendshëm ose të jashtëm janë kongruent, atëherë dy drejtëzat janë paralele”.
“Nëse dy kende përgjegjës janë congruent, ateherë dy drejtëzat janë paralele”.
“Nëse kënde të njëanshëm të brendshëm ose të jashtëm janë me shumë 180º (shtues), atëherë dy drejtëzat janë paralele”.