Kriteret e paralelizmit te dy drejtezave

Drejtëzat paralele

Përkufizim: “Dy drejtëza të planit quhen paralele, nëse ato nuk kanë asnjë pikë të përbashkët”.

Kemi në figurë dy drejtëza paralele:

Këndet që formohen nga prerja e dy drejtëzave më një të tretë

Le të kemi në plan dy drejtëza çfarëdo a dhe b dhe një drejtëz c, që pret këto dy drejtëza, po në pika të ndryshme. Drëjtëza c quhet prerëse. Nga prerja e drejtëzave a, b me prerësen c formohen 8 kënde, të cilët i kemi shënuar me numra.

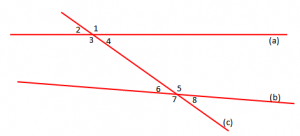
Nga klasa e shtatë, dimë që kur një drejtëz e tretë pret dy drejtëza, formohen këto kënde:

Kënde përgjegjës ( $\displaystyle \angle 1$ me $\displaystyle \angle 1$ , $\displaystyle \angle$ me $\displaystyle \angle 1$ , $\displaystyle \angle 3$ me $\displaystyle \angle 7$ , $\displaystyle \angle 4$ me $\displaystyle \angle 8$ )

Kënde ndërrues të brendshëm ( $\displaystyle \angle 3$ me $\displaystyle \angle 5$ , $\displaystyle \angle 4$ me $\displaystyle \angle 6$ )

Kënde ndërrues të jashtëm ( $\displaystyle \angle 1$ me $\displaystyle \angle 7$ , $\displaystyle \angle 2$ me $\displaystyle \angle 8$ )

Kënde të njëanshëm të brendshëm ( $\displaystyle \angle 4$ me $\displaystyle \angle 5$ , $\displaystyle \angle 3$ me $\displaystyle \angle 6$ )

Kushte të mjaftueshme për paralelizmin e drejtëzave

Teoremë 1: “Nëse nga prerja e dy drejtëzave me një prerëse formohen dy kënde ndërrues të brendshëm kongruentë, atëherë drejtëzat janë paralele”.

Teoremë 2: “Nëse nga prerja e dy drejtëzave me një prerëse formohen dy kënde përgjegjës kongruentë, atëherë këto drejtëza janë paralele”.

Shembull 1

Kemi dy drejtëza që priten nga një e trëtë dhe formohen 8 kënde, si në figurën më poshtë:

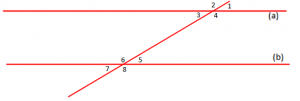
Kemi $\displaystyle \hat{1}=50{}^\text{o}$ dhe $\displaystyle \hat{8}=130{}^\text{o}$ .

Vërtetoni që $\displaystyle a//b$ .

Zgjidhje

Nga ushtrimi kemi:

$\displaystyle \hat{1}$ është i kundërt në kulm me $\displaystyle \hat{3}$ , ndaj $\displaystyle \hat{1}=\hat{3}=50{}^\text{o}$ .

$\displaystyle \hat{5}+\hat{8}=180{}^\text{o}$ , ndaj do të kemi:
$\displaystyle \hat{5}=180{}^\text{o}-\hat{8}$
$\displaystyle =180{}^\text{o}-130{}^\text{o}=50{}^\text{o}$

Pra, kemi: $\displaystyle \hat{3}=50{}^\text{o}$ dhe $\displaystyle \hat{5}=50{}^\text{o}$ të cilët janë kënde ndërrues të brendshëm dhe nga teorema, meqë janë kende ndërrues të brendshëm kongruentë, atëherë drejtëzat a dhe b janë paralele.

Veti të drejtëzave paralele

Aksioma e paraleleve: “Nëpër një pikë që nuk shtrihet në një drejtëz, nuk mund të hiqet më tepër se një drejtëz paralele me drejtëzn e dhënë”.

Teoremat mbi këndet që formojnë dy drejtëza paralele me një prerëse

Teoremë 3 (e anasjellta e teoremës 1): “Nëse dy drejtëza paralele priten nga një prerëse, çdo çift këndesh ndërrues të brendshëm janë kongruentë”.

Kemi figurën:

Nëse $\displaystyle a//b$ , atëherë do të kemi: $\displaystyle \hat{3}=\hat{5}$ dhe $\displaystyle \hat{4}=\hat{6}$

Teoremë 4 (e anasjellta e teoremës 2): “Nëse dy drejtëza paralele janë prerë nga një prerëse, çdo dy kënde përgjegjës janë kongruentë”.

Kemi figurën:

Nëse $\displaystyle a//b$ , atëherë do të kemi: $\displaystyle \hat{1}=\hat{5}$ , $\displaystyle \hat{2}=\hat{6}$ , $\displaystyle \hat{3}=\hat{7}$ dhe $\displaystyle \hat{4}=\hat{8}$