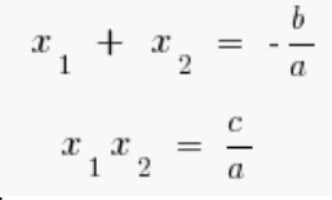
Formulat e Vietes | Matematika

Formulat e Vietes na ndihmojnë të gjejmë shumën dhe prodhimin e rrënjëve të ekuacionit te fuqise se dyte, kur ato ekzistojnë pa i gjetur më parë rrënjët.

Formulat e Vietes janë:

$\displaystyle {{x}_{1}}+{{x}_{2}}=-\frac{b}{a}$ dhe $\displaystyle {{x}_{1}}\cdot {{x}_{2}}=\frac{c}{a}$ .

Vërtetim

$\displaystyle {{x}_{1}}+{{x}_{2}}$

Duke mbledhur anë për anë do të kemi:

$\displaystyle {{x}_{1}}+{{x}_{2}}=\frac{-b-\sqrt{D}}{2a}+\frac{-b+\sqrt{D}}{2a}$

$\displaystyle =\frac{-b-\sqrt{D}-b+\sqrt{D}}{2a}$

$\displaystyle =\frac{-2b}{2a}=-\frac{b}{a}$

$\displaystyle {{x}_{1}}\cdot {{x}_{2}}$

$\displaystyle {{x}_{1}}\cdot {{x}_{2}}=\left( \frac{-b-\sqrt{D}}{2a} \right)\cdot \left( \frac{-b+\sqrt{D}}{2a} \right)$

Nga formula e diferencës së katrorit do të kemi:

$\displaystyle \left( \frac{-b-\sqrt{D}}{2a} \right)\cdot \left( \frac{-b+\sqrt{D}}{2a} \right)=\frac{{{\left( -b \right)}^{2}}-{{\left( \sqrt{D} \right)}^{2}}}{4{{a}^{2}}}$

$\displaystyle =\frac{{{b}^{2}}-D}{4{{a}^{2}}}$

Zëvëndësojmë formulën e dallorit dhe do të kemi:

$\displaystyle \frac{{{b}^{2}}-D}{4{{a}^{2}}}=\frac{{{b}^{2}}-\left( {{b}^{2}}-4ac \right)}{4{{a}^{2}}}$

$\displaystyle =\frac{-4ac}{4{{a}^{2}}}=-\frac{c}{a}$

Teoremë: “Nëse numrat m, n kanë shumën p dhe prodhimin q, atëherë këta numra janë rrënjë të ekuacionit $\displaystyle {{x}^{2}}-px+q=0$ ”.