Teza e Matematikes. Matura 2018 (pyetjet me zhvillim)

Këtu do të zgjidhim ushtrimet me zhvillim nga teza e matures 2018.

Teza e matematikës u zhvillua në 13 qershor 2018 dhe informacionet janë marrë nga ministria e arsimit.

Ushtrimi 14

Gjeni bashkesine e përcaktimit për funksionin: $\displaystyle x=\frac{{{\log }_{2}}\left( x+1 \right)}{3-x}$

Zgjidhje

$\displaystyle {{K}_{1}}:x+1>0\Rightarrow x>-1$

$\displaystyle {{E}_{1}}=\left] -1,+\infty \right[$

$\displaystyle {{K}_{2}}:3-x\ne 0\Rightarrow x\ne 3$

$\displaystyle {{E}_{2}}=R-\left\{ 3 \right\}$

$\displaystyle E={{E}_{1}}\cap {{E}_{2}}$

$\displaystyle E=\left] -1,3 \right[\cup \left] 3,+\infty \right[$

Ushtrimi 15

Gjeni vlerën e parametrit A, që funksioni i mëposhtëm të jetë i vazhdueshëm në pikën $\displaystyle x=0$ .

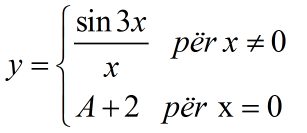
Zgjidhje

Që funksioni të jetë i vazhdueshëm në x=0, duhet të plotësohen njëherazi 3 kushte:

$\displaystyle f\left( 0 \right)=A+2$

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{\sin 3x}{x}=\frac{0}{0}=\underset{x\to 0}{\mathop{\lim 3}}\,\cdot \frac{\sin 3x}{3x}=3$

Funksioni është i vazhdueshëm në pikën $\displaystyle x=0$ , pra $\displaystyle \underset{x\to 0}{\mathop{\lim }}\,f\left( x \right)=\underset{x\to 0}{\mathop{\lim }}\,f\left( 0 \right)=3$

$\displaystyle A+2=3$

$\displaystyle A=1$

Përgjigje: Parametria A duhet të jetë 1, në mënyrë që funksioni të jetë i vazhdueshëm në pikën $\displaystyle x=0$ .

Ushtrimi 16

Për ç’vlerë të parametrit a, tangetja ndaj grafikut të funksionit $\displaystyle y=\frac{x-a}{2x}$ në pikën me abshisë $\displaystyle x=1$ , formon me boshtin ox këndin 45 gradë.

Zgjidhje

Kemi:

$\displaystyle y'=\frac{\left( x-a \right)'\cdot 2x-\left( x-a \right)\cdot \left( 2x \right)'}{4{{x}^{2}}}$

$\displaystyle y'=\frac{2x-\left( 2x-2a \right)}{4{{x}^{2}}}=\frac{2a}{4{{x}^{2}}}=\frac{a}{2{{x}^{2}}}$

$\displaystyle \frac{a}{{{x}^{2}}}=1$

$\displaystyle a=2$

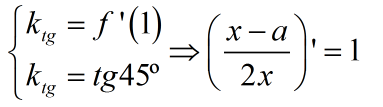
Përgjigje: Parametria a duhet të jetë 2.

Ushtrimi 17

Hidhen njeheresh 3 monedha. Sa eshte probabiliteti i ngjarjes qe ne dy dhe vetem dy prej tyre, te bjere stema?

Zgjidhje

Gjejmë hapësirën e rezultateve:

$\displaystyle n\left( H \right)=2\cdot 2\cdot 2=8$

Gjejmë numrin e mundësive që të bjerë 2 herë stema:

$\displaystyle A=\left\{ STS,SST,TSS \right\}$

$\displaystyle n\left( A \right)=3$

Gjejmë probabilitetin:

$\displaystyle P\left( A \right)=\frac{n\left( A \right)}{n\left( H \right)}=\frac{3}{8}$

Ushtrimi 18

Jepet funksioni $\displaystyle y=1-{{x}^{2}}$ në R.

a) Gjeni pikat ku grafiku pret boshtin OX.

b) Skiconi grafikun dhe gjeni syprinen e figures qe kufizohet nga grafiku I funksionit te dhene, dhe nga drejteza $\displaystyle y=-3$

Zgjidhje

a) Për të gjetur pikat ku grafiku pret boshtin Ox, zgjidhim sistemin:

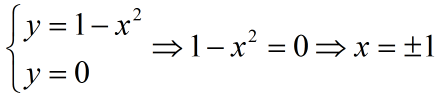
Pikat ku grafiku pret boshtin OX janë $\displaystyle \left( -1,0 \right)$ dhe $\displaystyle \left( 1,0 \right)$ .

b) Skicojmë grafikët e funksioneve mbi të njëjtin system koordinativ:

$\displaystyle y=1-{{x}^{2}}$ është parabolë me kulm K(0;1).

y = -3 drejtëz paralele me (OX).

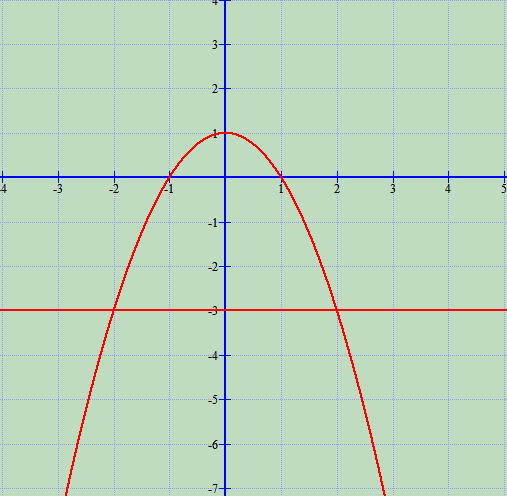
Gjejmë kufijtë e integrimit:

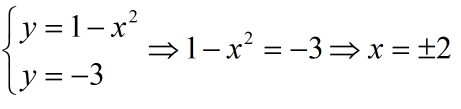
Meqenëse dy funksionet janë funksione çift atëherë:

$\displaystyle S=2\int\limits_{0}^{2}{\left[ 1-{{x}^{2}}-\left( -3 \right) \right]}dx=2\int\limits_{0}^{2}{\left[ 4-{{x}^{2}} \right]}dx$

$\displaystyle =2\left( 4x-\frac{{{x}^{3}}}{3} \right)|_{0}^{2}$

$\displaystyle =2\left( 8-\frac{8}{3} \right)-0=\frac{32}{3}$ njësi katrore.

Ushtrimi 19

Të zgjidhet ekuacioni $\displaystyle \left( 3x-6 \right)\sqrt{{{x}^{2}}-9}=0$

Zgjidhje

Në fillim gjejmë bashkësinë e përcaktimit të funksionit:

$\displaystyle {{x}^{2}}-9\ge 0$

$\displaystyle {{x}^{2}}-9=0$

$\displaystyle {{x}^{2}}=\pm 3$

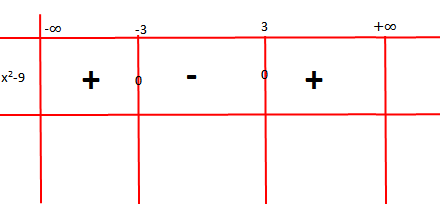
Nga studimi i shenjës, arrijmë në përfundimin që bashkësia e përcaktimit të funksionit është $\displaystyle x\in \left] -\infty ,-3 \right]\cup \left[ 3,+\infty \right[$ .

Tani zgjidhim ekuacionin duke barazuar secilën shprehje me zero:

Ekuacioni i parë:

$\displaystyle 3x-6=0$

$\displaystyle x=2$ , kjo nuk është zgjidhje për ekuacionin tonë, sepse nuk është pjesë e bashkësisë së përcaktimit.

Ekuacioni i dytë:

$\displaystyle {{x}^{2}}-9=0$

$\displaystyle {{x}^{2}}=9$

$\displaystyle x=\pm 3$ . Të dyja vlerat janë pjesë e bashkësisë së përcaktimit, ndaj zgjidhje të ekuacionit jane vlerat $\displaystyle x=-3$ dhe $\displaystyle x=3$ .

Ushtrimi 20

Jepet funksioni $\displaystyle y={{x}^{3}}-3{{x}^{2}}+5$ , $\displaystyle x\in R$ .

Studioni monotoninë e funksionit dhe gjeni ekstremumet.

Zgjidhje

Për të studiuar monotoninë e funksionit, studiojmë shenjën e derivatit

të pare.

Për çdo $\displaystyle x\in R$ , kemi $\displaystyle y'=3{{x}^{2}}-6x$

$\displaystyle f'\left( x \right)=0\Rightarrow 3{{x}^{2}}-6x=0$

$\displaystyle 3x\left( x-2 \right)=0$

$\displaystyle 3x=0$ ose $\displaystyle x-2=0$ . Pra, $\displaystyle x=0$ ose $\displaystyle x=2$ .

Studiojmë shenjën:

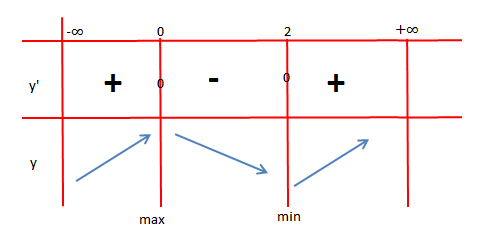
Pra, për $\displaystyle x\in \left] -\infty ,0 \right[\cup \left] 2,+\infty \right[$ kemi funksion rritës.

Për $\displaystyle x\in \left] 0,2 \right[$ kemi funksion zbritës.

$\displaystyle {{y}_{\max }}=f\left( 0 \right)=5$

$\displaystyle {{y}_{\min }}=f\left( 2 \right)=1$ .

Pra, pika maksimale është pika $\displaystyle \left( 0,5 \right)$ , ndërsa pika minimale është pika $\displaystyle \left( 2,1 \right)$ .

Ushtrimi 21

Jepen pikat A(1;2) dhe B(3;4) dhe C(a;0).

Për ç’vlerë të a-së, pika C gjendet në drejtëzën që kalon nga pikat A dhe B?

Zgjidhje

Gjejmë në fillim ekuacionin e drejtëzës AB:

$\displaystyle AB:\frac{x-{{x}_{A}}}{{{x}_{B}}-{{x}_{A}}}=\frac{y-{{y}_{A}}}{{{y}_{B}}-{{y}_{A}}}$

$\displaystyle AB:\frac{x-1}{3-1}=\frac{y-2}{4-2}$

$\displaystyle \left( AB \right):x-1=y-2$

$\displaystyle AB:x-1=y-2$

$\displaystyle AB:x-y+1=0$

Meqënëse pika C ndodhet në ekuacionin AB, atëherë pika e saj e vërteton ekuacionin. Pra, do të kemi:

$\displaystyle a-0+1=0$

$\displaystyle a+1=0$

$\displaystyle a=-1$ .

Ushtrimi 22

Jepet elipsi i cili pret boshtin OX ne piken (2;0).

a) Gjeni vlerën e a-së

b) Gjeni ekuacionin e tangentes ndaj elipsit, e cila është pingule me drejtezën $\displaystyle y=-x-1$

Zgjidhje

a) Në skajin e boshtit të madh: $\displaystyle \left( a,0 \right)=\left( 2,0 \right)$ . Pra, $\displaystyle a=2$ .

b) $\displaystyle \left( {{t}_{g}} \right)\bot \left( d \right)\Rightarrow {{k}_{tg}}\cdot {{k}_{d}}=-1$

Kemi $\displaystyle {{k}_{d}}=-1\Rightarrow {{k}_{tg}}=1$ .

Ekuacioni i tangents ka trajtën $\displaystyle y=x+t$ .

Nga kushti i tangjencës së drejtëzës me elipsin kemi: $\displaystyle {{a}^{2}}{{k}^{2}}+{{b}^{2}}={{t}^{2}}$ .

Ekuacionet e tangjenteve janë: $\displaystyle y=x-\sqrt{13}$ dhe $\displaystyle y=x+\sqrt{13}$ .

Ushtrimi 23

Rezultatet vjetore të nxënësve të një klase në matematikë, paraqiten në tabelën e mëposhtme.

Nota	4	5	6	7	8	9	10
Numri i nxënësve	4	6	5	5	4	4	2

Ç’përqindje e nxenesve kanë notë mesatare më të lartë se nota mesatare e klasës?

Zgjidhje

Gjejmë në fillim mesataren e klasës:

Notë më të lart se mesatarja kanë 15 nxënës, të cilët përbëjnë 50% të klasës.

Ushtrimi 24

Ne piramidën trekëndore, të gjitha faqet anësore formojnë kënde të barabarta me planin e bazës.

Tregoni, duke argumentuar, se ku ndodhet projeksioni i kulmit të piramidës, në planin e bazës.

Zgjidhje

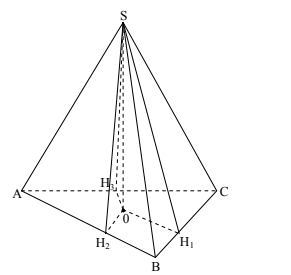
Ndërtojmë lartësinë $\displaystyle \left[ S{{H}_{1}} \right]$ të faqes SBC. Kemi:

U krijua këndi i prerjes së drejtë $\displaystyle \left( S{{{\hat{H}}}_{1}}O \right)$ .

Në të njëjtën mënyrë në dyfaqëshat e tjerë krijohen prerjet $\displaystyle \left( S{{{\hat{H}}}_{2}}O \right)$ dhe $\displaystyle \left( S{{{\hat{H}}}_{3}}O \right)$ .

Nga kongruenca e trekëndëshave $\displaystyle SO{{H}_{1}}$ ; $\displaystyle SO{{H}_{2}}$ ; $\displaystyle SO{{H}_{3}}$ $\displaystyle \Rightarrow \left[ O{{H}_{1}} \right]=\left[ O{{H}_{2}} \right]=\left[ O{{H}_{3}} \right]$ dhe $\displaystyle \left[ O{{H}_{1}} \right]\bot \left[ BC \right]$ ; $\displaystyle \left[ O{{H}_{2}} \right]\bot \left[ AB \right]$ dhe $\displaystyle \left[ O{{H}_{3}} \right]\bot \left[ AC \right]$ .