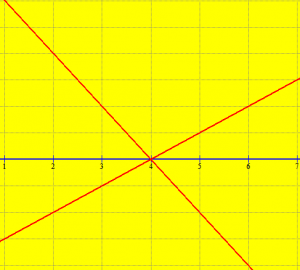
Ekuacioni i fuqise se pare me dy ndryshore. Grafiku i tij

Barazimin me dy ndryshore x, y, do ta quajmë ekuacion, nëse kërkohet për ç’vlera të x dhe y ai vërtetohet (kthehet në barazim numerik të vërtetë)

Përkufizim: “Çift i radhitur i dy numrave quhet zgjidhje e ekuacionit me dy ndryshore, nëse duke zëvëndësuar numrin e parë në vend të x dhe numrin e dytë në vend të y, ekuacioni vërtetohet”.

Për shembull, 2x + 3y = 7, një çift i radhitur mund të jetë (2, 1).

Grafiku i ekuacionit të fuqisë së parë me dy ndryshore

Çdo zgjidhje e ekuacionit të fuqisë së parë me dy ndryshore ax +bx +c = 0, është çift i radhitur numrash. Për çdo çift të tillë në planin ku është zgjedhur një system kënddrejt koordinativ xOy, i përgjigjet një pikë. Bashkësia e e këtyre pikave quhet grafik i këtij funksioni.

Shembull

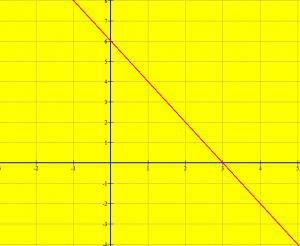
Përcaktoni grafikun e ekuacionit 2x + y – 6 = 0.

Zgjidhje

Grafiku i ekuacionit të fuqisë së parë me dy ndryshore është funksion linear. Për të ndërtuar grafikun linear mjafton të gjejmë 2 çifte të radhitura dhe ndërtojmë drejtëzën.

Zakonisht zëvëndësojmë x = 0 dhe y = 0 dhe gjejmë çiftet e radhitura dhe më pas ndërtojmë drejtëzën.

x = 0: $\displaystyle 2x+y-6=0$

$\displaystyle 0+y-6=0$

$\displaystyle y=6$

y = 0: $\displaystyle 2x+y-6=0$

$\displaystyle 2x+0-6=0$

$\displaystyle x=3$

Pra, kemi çiftet e radhitua (0, 6) dhe (5, 0). Ndërtojmë grafikun e funksionit linear $\displaystyle 2x+y-6=0$

Sistemi i ekuacioneve të fuqisë së parë me dy ndryshore. Zgjidhja grafike e tij

Sa herë që kërkohet të gjendet zgjidhjet e përbashkëta të dy ekuacioneve, themi që kërkohet të zgjidhet sistemi i këtyre ekuacioneve.

Për shembull, zgjidhje e përbashkët e ekuacioneve x + y = 5 dhe 2x-y=1 është çifti i radhitur (3, 2).

Një mënyrë për zgjidhjen e sistemit të ekuacioneve të fuqisë së parë me dy ndryshore është mënyra grafike.

Ndërtojmë në të njëjtin grafik ekuacionet që na kërkohen dhe pika e prerjes së tyre është zgjidhja e përbashkët e ekuacioneve.

Shembull

Gjeni zgjidhjen e ekuacioneve $\displaystyle 2x+y=8$ dhe $\displaystyle x-y=4$

Zgjidhje

Ndërtojmë sistemin e ekuacioneve:

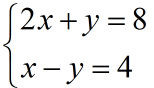
Pasi zëvëndësojmë x dhe y me 0, ndërtojmë çiftet e radhitura (0, 8) dhe (4, 0).

Ndërtojmë grafikun e funksionit: