
Zgjidhja e ekuacionit të fuqisë së parë me një ndryshore
Ekuacioni i fuqisë së parë me një ndryshore mund të shkruhet në formën
AX + B = 0
Veti të ekuacioneve
- Vetia e mbledhjes
Nëse A = B, është i vërtetë barazimi:
A + C = B + C
dhe A – C = B – C
- Vetia e shumëzimit
Nëse A = B, është i vërtetë barazimi:
A ∙ C = B ∙ C
dhe
Keshille! Per ushtrime te zgjidhura me ekuacione klikoni ushtrime te zgjidhura
Nga vetia e parë rrjedh:
- Çdo kufizë e ekuacionit mund të kalojë nga njëra anë e ekuacionit në anën tjetër të tij, duke ia ndryshuar shenjën në të kundërt.
- Kufizat e njëjta (në shenjë e vlerë) në të dy anët e ekuacionit mund t’i hiqen ekuacionit.
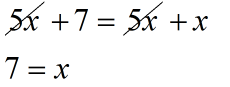
Nga vetia e dytë rrjedhin këto veti:
- Nëse të gjitha kufizat e një ekuacioni kanë një faktorë të përbashkët, atëherë, të gjitha kufizat e ekuacionit mund të pjesëtohen me atë faktor.
Për shembull, në ekuacionin
Duke pjestuar me faktorin 4, që është PMP (12, 4, 16, 20) = 4
kemi:
Keshille! Per ushtrime te zgjidhura me ekuacione klikoni ushtrime te zgjidhura
- Përpara të gjithë kufizave të një ekuacioni mund të shndërrohen shenjat në shenja të kundërta.
(është njësoj sikur të dy anët ti shumëzojmë me -1).
- Një ekuacion mund të lirohet nga kufizat thyesore që s’kanë ndryshore në emërues, duke shumëzuar të dy anët e ekuacionit me SH.V.P të emëruesve të kufizave të ekuacionit.
Për shembull, në ekuacionin
për të hequr emëruesit duhet të shumëzojmë me SHVP (7, 3, 2) = 42
Dhe në bazë të rregullit 2 kemi:
Duke ndjekur rregullat e ekuacionit, vazhdojmë transformimin e ekuacionit
Tani shumëzojmë me -1 për ta kthyer ekuacionin në trajtë të rregullt:
Keshille! Per ushtrime te zgjidhura me ekuacione klikoni ushtrime te zgjidhura
Numri i zgjidhjeve të ekuacionit të fuqisë së parë me një ndryshore
Tani do të mesojmë se çfarë kushtesh duhet të plotësojë një ekuacion I fuqisë së parë me një ndryshore, kur ai merr trajtën ax = b.
-
Ekuacioni ka një rrënjë kur:
ose
Forma që merr ekuacioni në këto raste është:
, kur
dhe
, kur b = 0
-
Ekuacioni ka një pafundësi rrënjësh kur:
a = 0 dhe b = 0
Në këtë rast do të kishim:
, ndaj ekuacioni ka një pafundësi zgjidhjesh.
-
Ekuacioni s’ka rrënjë kur:
a = 0,
Në këtë rast do të kishim:
0 ∙ x = b
0 = b (ne kemi kushtin që ), ndaj ekuacioni s’ka zgjidhje.

